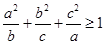题目内容
已知a,b,c为正数,且满足acos2θ+bsin2θ<c,求证: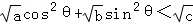
由柯西不等式定理构造不等式 ≤[(
≤[(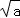 cosθ)2+(
cosθ)2+(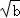 sinθ)2]
sinθ)2]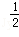 (cos2θ+sin2θ)
(cos2θ+sin2θ)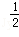 直接证明即可.
直接证明即可.
解析试题分析:证明:由柯西不等式,得 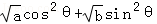
≤[(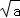 cosθ)2+(
cosθ)2+(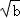 sinθ)2]
sinθ)2]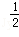 (cos2θ+sin2θ)
(cos2θ+sin2θ)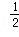
=(acos2θ+bsin2θ)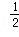
<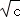 .…(10分)
.…(10分)
考点:柯西不等式在函数极值中的应用;柯西不等式的几何意义
点评:本题考查了柯西不等式证明不等式的方法,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 b2+
b2+ c2+m-1=0.
c2+m-1=0.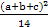 .
.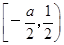 时,f(x)≤g(x),求a的取值范围.
时,f(x)≤g(x),求a的取值范围.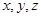 ,
,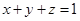 ,求证:
,求证: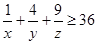 ;
;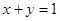 ,求
,求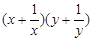 的最小值。
的最小值。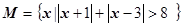 ,
,
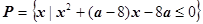 的前提下,求a的一个值,是它成为
的前提下,求a的一个值,是它成为 的一个充分但不必要条件。
的一个充分但不必要条件。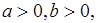 求证:
求证: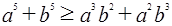
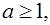 求证:
求证: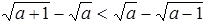
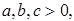 求证:
求证: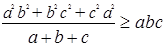
 的不等式:
的不等式: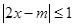 的整数解有且仅有一个值为2.
的整数解有且仅有一个值为2.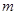 的值;(2)在(1)的条件下,解不等式:
的值;(2)在(1)的条件下,解不等式: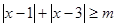 .
. 是正实数, 求证:
是正实数, 求证: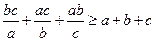 .
.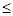
 ;
;