题目内容
19.已知函数f(x)=$\frac{1}{3}$x3-ax2-3a2x+b(a,b∈R).(Ⅰ)若曲线f(x)在点(1,f(1))处的切线方程为y=1,求a,b的值;
(Ⅱ)求f(x)的单调区间及极值.
分析 (Ⅰ)求出函数的导数,求得切线的斜率和切点,由切线的方程,可得a,b的方程,解方程可得a,b的值;
(Ⅱ)求得导数,讨论a=0,a>0,a<0,由导数大于0,可得增区间,导数小于0,可得减区间,进而得到极值.
解答 解:(Ⅰ)函数f(x)=$\frac{1}{3}$x3-ax2-3a2x+b的导数为f′(x)=x2-2ax-3a2,
f(x)在点(1,f(1))处的切线斜率为1-2a-3a2,
由切线方程为y=1,可得f(1)=1,f′(1)=0,
即为$\frac{1}{3}$-a-3a2+b=1,1-2a-3a2=0,
解得a=-1,b=$\frac{8}{3}$或a=$\frac{1}{3}$,b=$\frac{4}{3}$;
(Ⅱ)f′(x)=x2-2ax-3a2=(x-3a)(x+a),
当a=0时,f′(x)≥0,f(x)在R上递增;
当a>0时,-a<3a,当x>3a或x<-a时,f′(x)>0,f(x)递增;
当-a<x<3a时,f′(x)<0,f(x)递减.
即有x=-a处取得极大值,且为b+$\frac{5}{3}$a3;x=3a处取得极小值,且为b-9a3.
当a<0时,-a>3a,当x>-a或x<3a时,f′(x)>0,f(x)递增;
当3a<x<-a时,f′(x)<0,f(x)递减.
即有x=-a处取得极小值,且为b+$\frac{5}{3}$a3;x=3a处取得极大值,且为b-9a3.
综上可得,a=0时,f(x)的增区间为(-∞,+∞),无极值;
a>0时,f(x)的增区间为(-∞,-a),(3a,+∞),减区间为(-a,3a),
极小值为b-9a3,极大值为b+$\frac{5}{3}$a3;
a<0时,f(x)的减区间为(-∞,3a),(-a,+∞),增区间为(3a,-a),
极大值为b-9a3,极小值为b+$\frac{5}{3}$a3.
点评 本题考查导数的运用:求切线的斜率和单调区间、极值,考查分类讨论的思想方法,以及运算求解能力,属于中档题.

 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
| A. | 2 | B. | 4 | C. | 8 | D. | 16 |
| A. | 周期为$\frac{π}{3}$的函数 | B. | 周期为$\frac{π}{2}$的函数 | C. | 周期为π的函数 | D. | 周期为2π的函数 |
| A. | -$\frac{3}{4}$ | B. | 7 | C. | -$\frac{7}{8}$ | D. | $\frac{7}{8}$ |
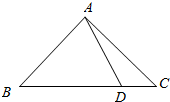 如图,在△ABC中,已知B=$\frac{π}{4}$,D是BC边上一点,AD=10,AC=14,DC=6,则AB=5$\sqrt{6}$.
如图,在△ABC中,已知B=$\frac{π}{4}$,D是BC边上一点,AD=10,AC=14,DC=6,则AB=5$\sqrt{6}$.