题目内容
如图，在直角三角形ABC中，D是斜边BC边上的中点，AC=8cm，BC=6cm，EC⊥平面ABC，EC=12cm，求 EA，EB，ED的长．
分析：连接CD，由题意可得：△AEC为直角三角形，再根据勾股定理求出EA，同理EB；根据直角三角形的性质可得CD=5cm，再利用线面垂直的性质与勾股定理求出ED的值．
解答：解：连接CD，
因为EC⊥平面ABC，AC?平面ABC，
所以EC⊥AC，
所以△AEC为直角三角形，并且∠ACE=90°，
又因为AC=8cm，EC=12cm，
所以EA=
=4
；
因为EC⊥平面ABC，BC?平面ABC，
所以EC⊥BC，
所以△EBC为直角三角形，并且∠BCE=90°，
又因为BC=6cm，EC=12cm，
所以EB=
=6
；
因为在直角三角形ABC中，AC=8cm，BC=6cm，
所以AB=10cm，
又因为D是斜边BC边上的中点，
所以CD=5cm，
因为EC⊥平面ABC，CD?平面ABC，
所以△EDC为直角三角形，并且∠DCE=90°，
因为EC=12cm，
所以ED=
=13．
因为EC⊥平面ABC，AC?平面ABC，
所以EC⊥AC，
所以△AEC为直角三角形，并且∠ACE=90°，
又因为AC=8cm，EC=12cm，
所以EA=
| AC2+EC2 |
| 13 |
因为EC⊥平面ABC，BC?平面ABC，
所以EC⊥BC，
所以△EBC为直角三角形，并且∠BCE=90°，
又因为BC=6cm，EC=12cm，
所以EB=
| BC2+EC2 |
| 5 |
因为在直角三角形ABC中，AC=8cm，BC=6cm，
所以AB=10cm，
又因为D是斜边BC边上的中点，
所以CD=5cm，
因为EC⊥平面ABC，CD?平面ABC，
所以△EDC为直角三角形，并且∠DCE=90°，
因为EC=12cm，
所以ED=
| DC2+EC2 |
点评：此题主要考查线面垂直的判定和性质定理，并且能够熟练利用勾股定理求线段的长度，属基础题．
练习册系列答案
相关题目
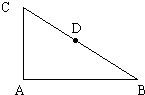如图，在直角三角形ABC中，∠BAC=90°，D为BC的中点，
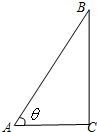如图，在直角三角形ABC中，斜边AB=4．设角A=θ，△ABC的面积为S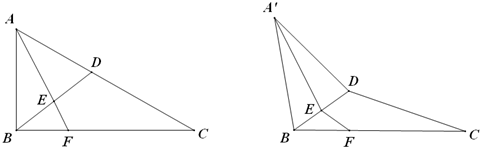
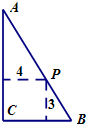（2012•贵州模拟）如图，在直角三角形ABC的斜边AB上有一点P，它到这个三角形两条直角边的距离分别为4和3，则△ABC面积的最小值是（ ）
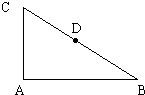如图，在直角三角形ABC中，∠BAC=90°，D为BC的中点，
，
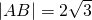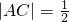，以A、B为焦点的椭圆经过点C．
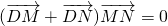？若存在，求出直线l斜率的取值范围；若不存在，请说明理由．