Question

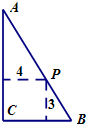（2012•贵州模拟）如图，在直角三角形ABC的斜边AB上有一点P，它到这个三角形两条直角边的距离分别为4和3，则△ABC面积的最小值是（　　）

A．12

B．18

C．24

D．48

Answer 1

分析：设∠B=θ，将BC、AC用θ表示出来，然后根据直角三角形的面积公式表示其面积，最后利用基本不等式求出最值即可．

解答：解：设∠B=θ，则BC=4+

3

tanθ

，AC=3+4tanθ，θ∈（0，

π

2

）
∴S_△ABC=

1

2

AC×BC=

1

2

（=3+4tanθ）（4+

3

tanθ

）=

1

2

（24+16tanθ+

9

tanθ

）≥

1

2

（24+2

16×9

）=24
当且仅当tanθ=

3

4

时取等号
故选C．

点评：本题主要考查了三角形的面积，以及基本不等式的应用，同时考查了计算能力，属于基础题．