题目内容
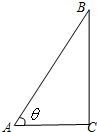如图，在直角三角形ABC中，斜边AB=4．设角A=θ，△ABC的面积为S（1）试用θ表示S，并求S的最大值；
（2）计算
| AB |
| AC |
| BC |
| BA |
分析：（1）先在直角三角形ABC中，求出|AC|=4cosθ，再代入三角形的面积计算公式即可用θ表示出S，最后结合三角函数求最值的方法可求S的最大值；
（2）直接利用
=-
以及
=-
把原问题转化，再结合向量的加法公式即可求出结论．
（2）直接利用
| BC |
| CB |
| BA |
| AB |
解答：解：（1）因为在直角三角形ABC中，斜边AB=4．角A=θ．
所以有：|AC|=4cosθ，
故S=
|AB|•|AC|•sinθ
=
×4×4cosθ•sinθ
=8sinθ•coθ
=4sin2θ．
当2θ=
即θ=
时，
△ABC的面积S有最大值4．
（2）∵
•
+
•
=
•
+
•
=
•（
+
）
=
2=42=16．
∴
•
+
•
的值为16．
所以有：|AC|=4cosθ，
故S=
| 1 |
| 2 |
=
| 1 |
| 2 |
=8sinθ•coθ
=4sin2θ．
当2θ=
| π |
| 2 |
| π |
| 4 |
△ABC的面积S有最大值4．
（2）∵
| AB |
| AC |
| BC |
| BA |
=
| AB |
| AC |
| CB |
| AB |
=
| AB |
| AC |
| CB |
=
| AB |
∴
| AB |
| AC |
| BC |
| BA |
点评：本题主要考查三角函数在实际生活中的运用以及向量知识的应用．解决第二问的关键在于利用
=-
以及
=-
把原问题转化，从而用已知条件AB=4求出结论．
| BC |
| CB |
| BA |
| AB |
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案
相关题目
如图，在直角三角形ABC中，∠BAC=90°，D为BC的中点，
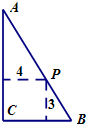（2012•贵州模拟）如图，在直角三角形ABC的斜边AB上有一点P，它到这个三角形两条直角边的距离分别为4和3，则△ABC面积的最小值是（ ）
如图，在直角三角形ABC中，∠BAC=90°，D为BC的中点，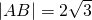
，
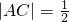，以A、B为焦点的椭圆经过点C．
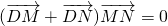？若存在，求出直线l斜率的取值范围；若不存在，请说明理由．