题目内容
如图:在直角三角形ABC中,已知AB=a,∠ACB=30°,∠B=90°,D为AC的中点,E为BD的中点,AE的延长线交BC于F,将△ABD沿BD折起,二面角A′-BD-C的大小记为θ.
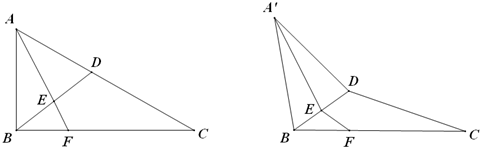
(1)求证:平面A′EF⊥平面BCD;
(2)当A′B⊥CD时,求sinθ的值;
(3)在(2)的条件下,求点C到平面A′BD的距离.

(1)求证:平面A′EF⊥平面BCD;
(2)当A′B⊥CD时,求sinθ的值;
(3)在(2)的条件下,求点C到平面A′BD的距离.
分析:(1)可以先证明△ABD为等边三角形,从而可得BD⊥AE,BD⊥EF,根据线面垂直的判定可得BD⊥面AEF,进而根据面面垂直的判定可得面AEF⊥面BCD.
(2)由(1)的证明可得∠A′EF为二面角A-BD-C的平面角.过A作AO⊥面BCD,垂足为O.由于面AEF⊥面BCD,所以O在FE上,连BO交CD延长线于M,从而当AB⊥CD时,由三垂线定理的逆定理得BM⊥CM,由此可求得sinθ的值;
(3):利用体积相等求点C到平面A′BD的距离即可.
(2)由(1)的证明可得∠A′EF为二面角A-BD-C的平面角.过A作AO⊥面BCD,垂足为O.由于面AEF⊥面BCD,所以O在FE上,连BO交CD延长线于M,从而当AB⊥CD时,由三垂线定理的逆定理得BM⊥CM,由此可求得sinθ的值;
(3):利用体积相等求点C到平面A′BD的距离即可.
解答: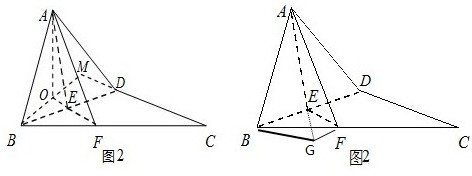 解:(1)证明:由△PBA为Rt△,
解:(1)证明:由△PBA为Rt△,
∠C=30° AB=
AC
∵D为AC中点,
∴AD=BD=DC
∵△ABD为正三角形
又∵E为BD中点
∴BD⊥AE’BD⊥EF
又由A’E∩EF=E,
且A’E、EF∈平面A’EF,BD⊥平面A’EF
∴面A’EF⊥平面BCD
(2)由(Ⅰ)的证明可得∠A′EF为二面角A-BD-C的平面角.过A作AO⊥面BCD,垂足为O.
∵面A′EF⊥面BCD,
∴O在FE上,连BO交CD延长线于M,
当A′B⊥CD时,由三垂线定理的逆定理得BM⊥CM,
∴O为翻折前的等边三角形△ABD的中心.
则OE=
AE,cosθ=-
⇒sinθ=
.
因此当A′B⊥CD时,sinθ=
…(7分)
(3)∵S△A′BD=
•a•a•sin60°=
a2;
A′E=
a,A′O=
AE=
a,
S△BCD=
S△ABC=
×
•a•
a=
a2;
∵VC-A′BD=VA′-BCD
∴
•h•S△A′BD=
•A′O•S△BCD⇒h=
a.
即所求距离为:
a.
 解:(1)证明:由△PBA为Rt△,
解:(1)证明:由△PBA为Rt△,∠C=30° AB=
| 1 |
| 2 |
∵D为AC中点,
∴AD=BD=DC
∵△ABD为正三角形
又∵E为BD中点
∴BD⊥AE’BD⊥EF
又由A’E∩EF=E,
且A’E、EF∈平面A’EF,BD⊥平面A’EF
∴面A’EF⊥平面BCD
(2)由(Ⅰ)的证明可得∠A′EF为二面角A-BD-C的平面角.过A作AO⊥面BCD,垂足为O.
∵面A′EF⊥面BCD,
∴O在FE上,连BO交CD延长线于M,
当A′B⊥CD时,由三垂线定理的逆定理得BM⊥CM,
∴O为翻折前的等边三角形△ABD的中心.
则OE=
| 1 |
| 3 |
| 1 |
| 3 |
2
| ||
| 3 |
因此当A′B⊥CD时,sinθ=
2
| ||
| 3 |
(3)∵S△A′BD=
| 1 |
| 2 |
| ||
| 4 |
A′E=
| ||
| 2 |
2
| ||
| 3 |
| ||
| 3 |
S△BCD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| ||
| 4 |
∵VC-A′BD=VA′-BCD
∴
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 3 |
即所求距离为:
| ||
| 3 |
点评:本题以平面图形为载体,考查图形的翻折,关键是搞清翻折前后有关元素的变与不变,考查面面角,考查线面角,关键是正确作出相应的角.

练习册系列答案
相关题目
 如图,在直角三角形ABC中,∠BAC=90°,D为BC的中点,
如图,在直角三角形ABC中,∠BAC=90°,D为BC的中点, 如图,在直角三角形ABC中,斜边AB=4.设角A=θ,△ABC的面积为S
如图,在直角三角形ABC中,斜边AB=4.设角A=θ,△ABC的面积为S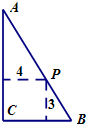 (2012•贵州模拟)如图,在直角三角形ABC的斜边AB上有一点P,它到这个三角形两条直角边的距离分别为4和3,则△ABC面积的最小值是( )
(2012•贵州模拟)如图,在直角三角形ABC的斜边AB上有一点P,它到这个三角形两条直角边的距离分别为4和3,则△ABC面积的最小值是( )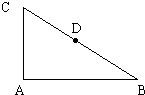 如图,在直角三角形ABC中,∠BAC=90°,D为BC的中点,
如图,在直角三角形ABC中,∠BAC=90°,D为BC的中点,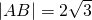 ,
,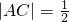 ,以A、B为焦点的椭圆经过点C.
,以A、B为焦点的椭圆经过点C. ?若存在,求出直线l斜率的取值范围;若不存在,请说明理由.
?若存在,求出直线l斜率的取值范围;若不存在,请说明理由.