题目内容
求下列函数的单调递增区间:
(1)y=(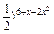 ;(2)y=2
;(2)y=2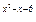 .
.
(1)y=(
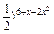 ;(2)y=2
;(2)y=2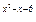 .
.(1)y=(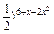 的单调递增区间为[
的单调递增区间为[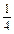 ,+∞)(2)函数y=2
,+∞)(2)函数y=2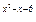 的单调递增区间是[
的单调递增区间是[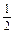 ,+∞)
,+∞)
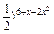 的单调递增区间为[
的单调递增区间为[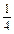 ,+∞)(2)函数y=2
,+∞)(2)函数y=2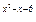 的单调递增区间是[
的单调递增区间是[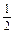 ,+∞)
,+∞)(1)函数的定义域为R.
令u=6+x-2x2,则y=(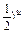 .
.
∵二次函数u=6+x-2x2的对称轴为x=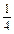 ,
,
在区间[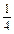 ,+∞)上,u=6+x-2x2是减函数,
,+∞)上,u=6+x-2x2是减函数,
又函数y=(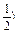 u是减函数,
u是减函数,
∴函数y=(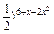 在[
在[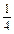 ,+∞)上是增函数.
,+∞)上是增函数.
故y=(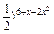 的单调递增区间为[
的单调递增区间为[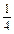 ,+∞).
,+∞).
(2)令u=x2-x-6,则y=2u,
∵二次函数u=x2-x-6的对称轴是x=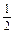 ,
,
在区间[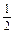 ,+∞)上u=x2-x-6是增函数.
,+∞)上u=x2-x-6是增函数.
又函数y=2u为增函数,
∴函数y=2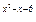 在区间[
在区间[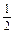 ,+∞)上是增函数.
,+∞)上是增函数.
故函数y=2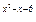 的单调递增区间是[
的单调递增区间是[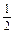 ,+∞).
,+∞).
令u=6+x-2x2,则y=(
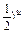 .
.∵二次函数u=6+x-2x2的对称轴为x=
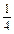 ,
,在区间[
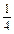 ,+∞)上,u=6+x-2x2是减函数,
,+∞)上,u=6+x-2x2是减函数,又函数y=(
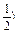 u是减函数,
u是减函数,∴函数y=(
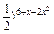 在[
在[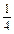 ,+∞)上是增函数.
,+∞)上是增函数.故y=(
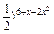 的单调递增区间为[
的单调递增区间为[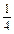 ,+∞).
,+∞).(2)令u=x2-x-6,则y=2u,
∵二次函数u=x2-x-6的对称轴是x=
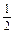 ,
,在区间[
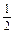 ,+∞)上u=x2-x-6是增函数.
,+∞)上u=x2-x-6是增函数.又函数y=2u为增函数,
∴函数y=2
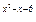 在区间[
在区间[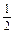 ,+∞)上是增函数.
,+∞)上是增函数.故函数y=2
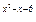 的单调递增区间是[
的单调递增区间是[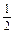 ,+∞).
,+∞).
练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目

 的单调区间
的单调区间 都有
都有 成立,求实数a的取值范围
成立,求实数a的取值范围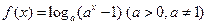
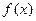 的定义域;
的定义域;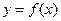 是奇函数,对于任意
是奇函数,对于任意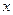 、
、 R都有
R都有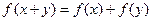 ,且当
,且当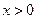 时,
时,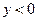 ,
,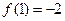 ,求函数
,求函数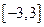 上的最大值和最小值.
上的最大值和最小值.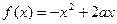 与
与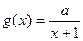 在区间
在区间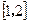 上都是减函数,则a的取值范围是( )
上都是减函数,则a的取值范围是( )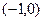
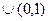 B
B 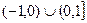 C
C 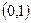 D
D 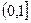
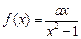 (
(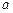 ≠0)在区间(-1,1)上的单调性。
≠0)在区间(-1,1)上的单调性。 满足:对任意实数
满足:对任意实数 ,当
,当 时,总有
时,总有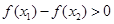 ,那么实数
,那么实数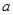 的取值范围是( )
的取值范围是( )


