题目内容
11．已知非钝角三角形ABC中，∠B=60°，边AB减去BC的长等于AC边上的高，若sinC与-sinA分别是方程x2-mx+m2-$\frac{3}{4}$=0的两根，求实数m的值和角A，C的大小．分析 画出图形，利用直角三角形的边角关系结合已知条件列出方程组，求解即可．
解答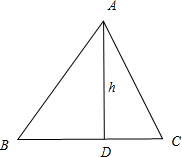 
解：设三角形ABC的AC边上的高为h，由∠B=60°，且三角形是非钝角三角形，
∴AB=$\frac{h}{sinA}$，BC=$\frac{h}{sinC}$，由题意可得，AB-BC=h，
∴$\frac{h}{sinA}-\frac{h}{sinC}=h$∴sinC-sinA=sinCsinA，
又sinC与-sinA分别是方程x2-mx+m2-$\frac{3}{4}$=0的两根，
∴sinC-sinA=m，与-sinCsinA=m2-$\frac{3}{4}$，可得$\frac{3}{4}$-m2=m，
解得m=$\frac{1}{2}$，（m=-$\frac{3}{2}$舍去）
sinCsinA=$\frac{1}{2}$，sinA（sinA+$\frac{1}{2}$）=$\frac{1}{2}$，
2sin2A+sinA-1=0，可得sinA=$\frac{1}{2}$，sinA=-1（舍去）．
所以A=30°，C=90°．
点评 本题考查三角形的解法，三角函数与才的关系，考查计算能力．
练习册系列答案
相关题目
16．已知函数f（x）=2sin（ωx）（其中常数ω＞0），若存在x1∈[-$\frac{2π}{3}$，0]，x2∈（0，$\frac{π}{4}$]，使f（x1）=f（x2），则ω的取值范围为（ ）
| A． | （$\frac{3}{2}$，4） | B． | （$\frac{3}{2}$，+∞） | C． | （4，+∞） | D． | （0，$\frac{3}{2}$） |
如图，用一边长为$\sqrt{2}$的正方形硬纸，按各边中点垂直折起四个小三角形，做成一个蛋巢，将表面积为4π的鸡蛋（视为球体）放入其中，蛋巢形状保持不变，则鸡蛋中心（球心）与蛋巢底面的距离为$\frac{\sqrt{3}}{2}$+$\frac{1}{2}$．
如图，在正四棱柱ABCD-A1B1C1D1中，AB=1，AA1=2，点M为CC1的中点，则点D1到平面BDM的距离为$\frac{{2\sqrt{3}}}{3}$．