题目内容
函数f（x），g（x）在区间[a，b]上都有意义，且在此区间上
①f（x）为增函数，f（x）＞0；
②g（x）为减函数，g（x）＜0．
判断f（x）g（x）在[a，b]的单调性，并给出证明．
①f（x）为增函数，f（x）＞0；
②g（x）为减函数，g（x）＜0．
判断f（x）g（x）在[a，b]的单调性，并给出证明．
分析：令a≤x1＜x2≤b，由f（x）、g（x）的单调性可得f（x1）与f（x2）的大小，g（x2）与g（x1）的大小，通过作差可判断
f（x1）g（x1）-f（x2）g（x2）的符号，由单调性的定义可得结论．
f（x1）g（x1）-f（x2）g（x2）的符号，由单调性的定义可得结论．
解答：解：减函数，
令a≤x1＜x2≤b，则有f（x1）-f（x2）＜0，即可得0＜f（x1）＜f（x2）；
同理有g（x1）-g（x2）＞0，即可得g（x2）＜g（x1）＜0；
从而有f（x1）g（x1）-f（x2）g（x2）
=f（x1）g（x1）-f（x1）g（x2）+f（x1）g（x2）-f（x2）g（x2）
=f（x1）（g（x1）-g（x2））+（f（x1）-f（x2））g（x2）（*），
显然f（x1）（g（x1）-g（x2））＞0，（f（x1）-f（x2））g（x2）＞0，
从而（*）式＞0，
故函数f（x）g（x）为减函数．
令a≤x1＜x2≤b，则有f（x1）-f（x2）＜0，即可得0＜f（x1）＜f（x2）；
同理有g（x1）-g（x2）＞0，即可得g（x2）＜g（x1）＜0；
从而有f（x1）g（x1）-f（x2）g（x2）
=f（x1）g（x1）-f（x1）g（x2）+f（x1）g（x2）-f（x2）g（x2）
=f（x1）（g（x1）-g（x2））+（f（x1）-f（x2））g（x2）（*），
显然f（x1）（g（x1）-g（x2））＞0，（f（x1）-f（x2））g（x2）＞0，
从而（*）式＞0，
故函数f（x）g（x）为减函数．
点评：本题考查函数单调性的判断及其证明，属中档题，定义是解决问题的基本方法，解答本题的关键是对f（x1）g（x1）-f（x2）g（x2）进行添加项作出恰当变形．
练习册系列答案
相关题目
；
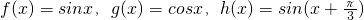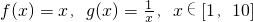的线性生成函数h（x），其中a＞0，b＞0．若h（x）≥b对a∈[1，2]恒成立，求实数b的取值范围．
；
的线性生成函数h（x），其中a＞0，b＞0．若h（x）≥b对a∈[1，2]恒成立，求实数b的取值范围．