题目内容
对于定义在区间[m,n]上的两个函数f(x)和g(x),如果对任意的x∈[m,n],均有不等式|f(x)-g(x)|≤1成立,则称函数f(x)与g(x)在[m,n]上是“友好”的,否则称“不友好”的.现在有两个函数f(x)=loga(x-3a)与g(x)=loga
(a>0,a≠1),给定区间[a+2,a+3].
(1)若f(x)与g(x)在区间[a+2,a+3]上都有意义,求a的取值范围;
(2)讨论函数f(x)与g(x)在区间[a+2,a+3]上是否“友好”.
| 1 | x-a |
(1)若f(x)与g(x)在区间[a+2,a+3]上都有意义,求a的取值范围;
(2)讨论函数f(x)与g(x)在区间[a+2,a+3]上是否“友好”.
分析:(1)欲使函数f(x)与g(x)在区间[a+2,a+3]上有意义,即使对数的真数大于0,建立关系式,解之即可;
(2)假设存在实数a,使得函数f(x)与g(x)在区间[a+2,a+3]上是“友好”的,建立关系式化简可得-1≤loga(x2-4ax+3a2)≤1,然后研究函数g(x)=loga(x2-4ax+3a2)在区间[a+2,a+3]上的单调性,建立关系式,解之即可.
(2)假设存在实数a,使得函数f(x)与g(x)在区间[a+2,a+3]上是“友好”的,建立关系式化简可得-1≤loga(x2-4ax+3a2)≤1,然后研究函数g(x)=loga(x2-4ax+3a2)在区间[a+2,a+3]上的单调性,建立关系式,解之即可.
解答:解:(1)函数f(x)与g(x)在区间[a+2,a+3]上有意义,
必须满足
⇒0<a<1
(2)假设存在实数a,使得函数f(x)与g(x)在区间[a+2,a+3]上是“友好”的,
则|f(x)-g(x)|=|loga(x2-4ax+3a2)|⇒|loga(x2-4ax+3a2)|≤1
即-1≤loga(x2-4ax+3a2)≤1(*)
因为a∈(0,1)⇒2a∈(0,2),而[a+2,a+3]在x=2a的右侧,
所以函数g(x)=loga(x2-4ax+3a2)在区间[a+2,a+3]上为减函数,从而
于是不等式(*)成立的充要条件是
⇒0<a≤
因此,当0<a≤
时,函数f(x)与g(x)在区间[a+2,a+3]上是“友好”的;当1>a>
时,函数f(x)与g(x)在区间[a+2,a+3]上是不“友好”的.
必须满足
|
(2)假设存在实数a,使得函数f(x)与g(x)在区间[a+2,a+3]上是“友好”的,
则|f(x)-g(x)|=|loga(x2-4ax+3a2)|⇒|loga(x2-4ax+3a2)|≤1
即-1≤loga(x2-4ax+3a2)≤1(*)
因为a∈(0,1)⇒2a∈(0,2),而[a+2,a+3]在x=2a的右侧,
所以函数g(x)=loga(x2-4ax+3a2)在区间[a+2,a+3]上为减函数,从而
|
于是不等式(*)成立的充要条件是
|
9-
| ||
| 12 |
因此,当0<a≤
9-
| ||
| 12 |
9-
| ||
| 12 |
点评:本题主要考查了函数单调性的判断与证明,以及新定义的运用,属于中档题.

练习册系列答案
相关题目
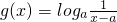 (a>0,a≠1),给定区间[a+2,a+3].
(a>0,a≠1),给定区间[a+2,a+3].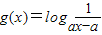 (a>0,a≠1),给定区间[a+2,a+3].
(a>0,a≠1),给定区间[a+2,a+3].