��Ŀ����
���ں���f��x����g��x����h��x�����������ʵ��a��b��ʹ��h��x��=af��x��+bg��x������ô��h��x��Ϊf��x����g��x�����������ɺ�����
��1�������������麯�������ж�h��x���Ƿ�ֱ�Ϊf��x����g��x�����������ɺ�������˵�����ɣ�
��һ�飺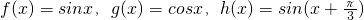 ��
��
�ڶ��飺f��x��=x2-x��g��x��=x2+x+1��h��x��=x2-x+1��
��2����֪f��x��=log2x��g��x��=log0.5x���������ɺ���Ϊh��x��������a=2��b=1��������ʽ3h2��x��+2h��x��+t��0��x��[2��4]���н⣬��ʵ��t��ȡֵ��Χ��
��3����֪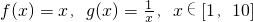 ���������ɺ���h��x��������a��0��b��0����h��x����b��a��[1��2]���������ʵ��b��ȡֵ��Χ��
���������ɺ���h��x��������a��0��b��0����h��x����b��a��[1��2]���������ʵ��b��ȡֵ��Χ��
�⣺��1����һ�飺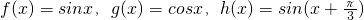 ��
��
��h��x��Ϊf��x����g��x�����������ɺ��������У�
����ʵ��a��b��ʹ��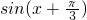 =asinx+bcosx��
=asinx+bcosx��
����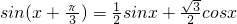 ����ʽ������
����ʽ������
��h��x��Ϊf��x����g��x�����������ɺ�����
�ڶ��飺f��x��=x2-x��g��x��=x2+x+1��h��x��=x2-x+1��
��h��x��Ϊf��x����g��x�����������ɺ��������У�
����ʵ��a��b��ʹ��x2-x+1=a��x2-x��+b��x2+x+1����
��x2-x+1=��a+b��x2-��a-b��x+b��
�� ���Dz����ܳ����ģ�
���Dz����ܳ����ģ�
��h��x����Ϊf��x����g��x�����������ɺ�����
��2����֪f��x��=log2x��g��x��=log0.5x���������ɺ���Ϊh��x��������a=2��b=1��
��h��x��=2log2x+log0.5x=log2x����x��[2��4]ʱ��1��h��x����2��
������ʽ3h2��x��+2h��x��+t��0��x��[2��4]���н⣬
��-t��3h2��x��+2h��x������Ҫ��-t��3h2��x��+2h��x����Сֵ���ɣ�
-t��5����t��-5
��ʵ��t��ȡֵ��Χt��-5��
��3������֪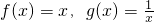 �����������ɺ���h��x��������a��0��b��0��
�����������ɺ���h��x��������a��0��b��0��
�ã�h��x��=ax+ ��
��
��h��x����b��a��[1��2]�������
��ax+ ��b��a��[1��2]�������
��b��a��[1��2]�������
bҪС�ڵ���ax+ ����Сֵ���ɣ�
����Сֵ���ɣ�
��b��2 ����
����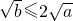 ��
��
����a��[1��2]����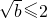 ����0��b��4
����0��b��4
��ʵ��b��ȡֵ��Χ��0��b��4��
��������1�����ڵ�һ�飺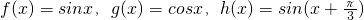 ���úͽǹ�ʽ���ɵõ�
���úͽǹ�ʽ���ɵõ�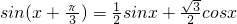 ����h��x��Ϊf��x����g��x�����������ɺ�����
����h��x��Ϊf��x����g��x�����������ɺ�����
�ڶ��飺f��x��=x2-x��g��x��=x2+x+1��h��x��=x2-x+1����h��x��Ϊf��x����g��x�����������ɺ��������У�
����ʵ��a��b��ʹ��x2-x+1=a��x2-x��+b��x2+x+1�������ù���a��b�ķ������⼴�ɵó�h��x����Ϊf��x����g��x�����������ɺ�����
��2���ȵõ�h��x��=2log2x+log0.5x=log2x����x��[2��4]ʱ��1��h��x����2��������ʽ3h2��x��+2h��x��+t��0��x��[2��4]���н⣬���û�Ԫ˼���϶��κ��������ʼ������ʵ��t��ȡֵ��Χ��
��3������֪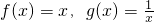 �����������ɺ���h��x��������a��0��b��0���ɵ�h��x��=ax+
�����������ɺ���h��x��������a��0��b��0���ɵ�h��x��=ax+ ���ٽ�Ϻ���h��x�����������ú��������Ľⷨ�������ʵ��b��ȡֵ��Χ��
���ٽ�Ϻ���h��x�����������ú��������Ľⷨ�������ʵ��b��ȡֵ��Χ��
��������С����Ҫ���麯������ʽ����⼰���÷�����������������⡢���DZ任������ʽ�Ȼ���֪ʶ����������������������黯����ת��˼�룬���ڻ����⣮
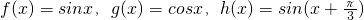 ��
����h��x��Ϊf��x����g��x�����������ɺ��������У�
����ʵ��a��b��ʹ��
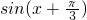 =asinx+bcosx��
=asinx+bcosx������
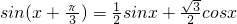 ����ʽ������
����ʽ��������h��x��Ϊf��x����g��x�����������ɺ�����
�ڶ��飺f��x��=x2-x��g��x��=x2+x+1��h��x��=x2-x+1��
��h��x��Ϊf��x����g��x�����������ɺ��������У�
����ʵ��a��b��ʹ��x2-x+1=a��x2-x��+b��x2+x+1����
��x2-x+1=��a+b��x2-��a-b��x+b��
��
 ���Dz����ܳ����ģ�
���Dz����ܳ����ģ���h��x����Ϊf��x����g��x�����������ɺ�����
��2����֪f��x��=log2x��g��x��=log0.5x���������ɺ���Ϊh��x��������a=2��b=1��
��h��x��=2log2x+log0.5x=log2x����x��[2��4]ʱ��1��h��x����2��
������ʽ3h2��x��+2h��x��+t��0��x��[2��4]���н⣬
��-t��3h2��x��+2h��x������Ҫ��-t��3h2��x��+2h��x����Сֵ���ɣ�
-t��5����t��-5
��ʵ��t��ȡֵ��Χt��-5��
��3������֪
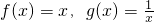 �����������ɺ���h��x��������a��0��b��0��
�����������ɺ���h��x��������a��0��b��0���ã�h��x��=ax+
 ��
����h��x����b��a��[1��2]�������
��ax+
 ��b��a��[1��2]�������
��b��a��[1��2]�������bҪС�ڵ���ax+
 ����Сֵ���ɣ�
����Сֵ���ɣ���b��2
 ����
����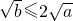 ��
������a��[1��2]����
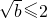 ����0��b��4
���ó���0��b��4��ʵ��b��ȡֵ��Χ��0��b��4��
��������1�����ڵ�һ�飺
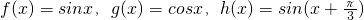 ���úͽǹ�ʽ���ɵõ�
���úͽǹ�ʽ���ɵõ�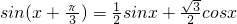 ����h��x��Ϊf��x����g��x�����������ɺ�����
����h��x��Ϊf��x����g��x�����������ɺ������ڶ��飺f��x��=x2-x��g��x��=x2+x+1��h��x��=x2-x+1����h��x��Ϊf��x����g��x�����������ɺ��������У�
����ʵ��a��b��ʹ��x2-x+1=a��x2-x��+b��x2+x+1�������ù���a��b�ķ������⼴�ɵó�h��x����Ϊf��x����g��x�����������ɺ�����
��2���ȵõ�h��x��=2log2x+log0.5x=log2x����x��[2��4]ʱ��1��h��x����2��������ʽ3h2��x��+2h��x��+t��0��x��[2��4]���н⣬���û�Ԫ˼���϶��κ��������ʼ������ʵ��t��ȡֵ��Χ��
��3������֪
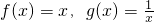 �����������ɺ���h��x��������a��0��b��0���ɵ�h��x��=ax+
�����������ɺ���h��x��������a��0��b��0���ɵ�h��x��=ax+ ���ٽ�Ϻ���h��x�����������ú��������Ľⷨ�������ʵ��b��ȡֵ��Χ��
���ٽ�Ϻ���h��x�����������ú��������Ľⷨ�������ʵ��b��ȡֵ��Χ����������С����Ҫ���麯������ʽ����⼰���÷�����������������⡢���DZ任������ʽ�Ȼ���֪ʶ����������������������黯����ת��˼�룬���ڻ����⣮

��ϰ��ϵ�д�
 ����ѧ��ţ��Ӣ��ϵ�д�
����ѧ��ţ��Ӣ��ϵ�д�
�����Ŀ