题目内容
已知点O为△ABC内一点,且
=m
+n
(其中m<0、n<0),S△AOB:S△AOC=2:3,则
=______.
| OA |
| OB |
| OC |
| m |
| n |
连接AO交BC于D,如下图所示:
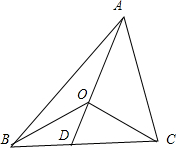
∵S△AOB:S△AOC=2:3,
∴S△ADB:S△ADC=2:3,
∴BD:CD=2:3,
则
=
+
又∵
与
共线
故
=
+
又∵
=m
+n
∴
=
故答案为:

∵S△AOB:S△AOC=2:3,
∴S△ADB:S△ADC=2:3,
∴BD:CD=2:3,
则
| OD |
| 3 |
| 5 |
| OB |
| 2 |
| 5 |
| OC |
又∵
| OA |
| OD |
故
| OA |
| 3 |
| 5 |
| λOB |
| 2 |
| 5 |
| λOC |
又∵
| OA |
| OB |
| OC |
∴
| m |
| n |
| 3 |
| 2 |
故答案为:
| 3 |
| 2 |

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案
相关题目
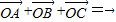 ,
,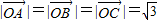 ,又
,又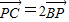 ,则
,则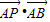 = _
= _ (其中m<0、n<0),S△AOB:S△AOC=2:3,则
(其中m<0、n<0),S△AOB:S△AOC=2:3,则 = .
= .