题目内容
已知点O为△ABC内一点，满足；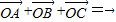
，
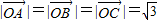，又
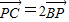，则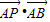
= _
【答案】分析：可判三角形为等边三角形，由正弦定理可得向量夹角的正弦值，进而可得余弦值，由数量积的定义可得答案．
解答：解：∵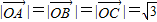
，∴O为△ABC的重心，
又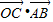
=
=
=
=
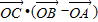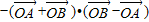
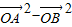=0可得
，
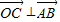同理可得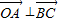
，
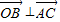，即O为垂心，
故△ABC为等边三角形，且边长为3
又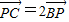
，故P为边BC的三等分点，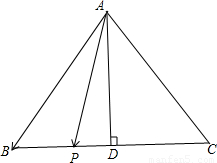
在直角三角形ADP中，易得AP=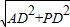
=
=
，
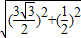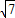进而可得sin∠APB=sin∠APD=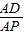
=
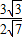
故在△ABP中，由正弦定理可得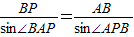
，
代入可得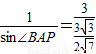
，解得sin∠BAP=
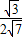，所以cos∠BAP=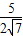
故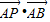
=
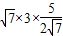=7.5
故答案为：7.5
点评：本题考查向量的数量积，涉及三角形形状的判断和正弦定理，属中档题．
解答：解：∵
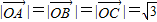，∴O为△ABC的重心，又
===
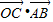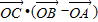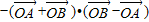
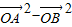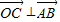==0可得，同理可得
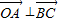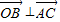，，即O为垂心，故△ABC为等边三角形，且边长为3
又
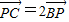，故P为边BC的三等分点，在直角三角形ADP中，易得AP=
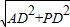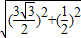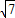==，进而可得sin∠APB=sin∠APD=
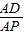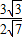
=故在△ABP中，由正弦定理可得
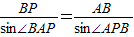，代入可得
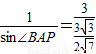，解得sin∠BAP=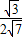，所以cos∠BAP=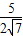故
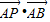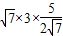==7.5故答案为：7.5
点评：本题考查向量的数量积，涉及三角形形状的判断和正弦定理，属中档题．
练习册系列答案
新课标同步训练系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
（其中m＜0、n＜0），S△AOB：S△AOC=2：3，则
= ．