题目内容
设※是集合A中元素的一种运算,如果对于任意的x,y∈A都有x※y∈A,则称运算※对集合A是封闭的,若M={x|x=a+
b,a,b∈Z},则对集合M不封闭的运算是( )
| 2 |
| A、加法 | B、减法 | C、乘法 | D、除法 |
分析:这是一个简单的合情推理问题,根据新运算的定义:果对于任意的x,y∈A都有x※y∈A,则称运算※对集合A是封闭的,要判断M={x|x=a+
b,a,b∈Z}时,则对集合M不封闭的运算,我们可以对答案中对应的运算逐一进行判断,易得到答案.
| 2 |
解答:解:设x=a+
b,y=c+
d(a、b、c、d∈Z),
则x+y=(a+c)+
(b+d)∈M,所以加法对集合M封闭;
x-y=(a-c)+
(b-d)∈M,∴减法对集合M封闭.
xy=(ac+2bd)+
•(ad+bc)∈M,∴乘法对集合M封闭.
=
=
=
+
,
故除法对集合M不封闭,
故答案选D.
| 2 |
| 2 |
则x+y=(a+c)+
| 2 |
x-y=(a-c)+
| 2 |
xy=(ac+2bd)+
| 2 |
| x |
| y |
a+
| ||
c+
|
(a+
| ||||
(c+
|
=
| ac-2bd |
| c2-2d2 |
| bc-ad |
| c2-2d2 |
| 2 |
故除法对集合M不封闭,
故答案选D.
点评:这是一道新运算类的题目,其特点一般是“新”而不“难”,处理的方法一般为:根据新运算的定义,将答案中的运算逐一代入进行验证,易得最终结果.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
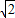 b,a,b∈Z},则对集合M不封闭的运算是( )
b,a,b∈Z},则对集合M不封闭的运算是( )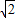 b,a,b∈Z},则对集合M不封闭的运算是( )
b,a,b∈Z},则对集合M不封闭的运算是( )