题目内容
设矩形ABCD(AB>AD)的周长为24,把它关于AC折起来,AB折过去后交CD于点P,如图,设AB=x,求△ADP的面积的最大值,及此时x的值.
△ADP面积的最大值为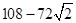 ,此时
,此时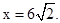
解析试题分析:22、(12分)∵AB=x,∴AD=12-x,又DP=PB′,AP=AB′-PB′=AB-DP,即AP=x-DP,
∴(12-x)2+PD2=(x-PD)2,得PD=12-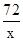 ,∵AB>AD,∴6<x<12,∴△ADP的面积S=
,∵AB>AD,∴6<x<12,∴△ADP的面积S=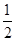 AD·DP
AD·DP
=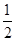 (12-x)(12-
(12-x)(12-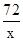 )=108-6(x+
)=108-6(x+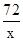 )≤108-6·
)≤108-6·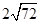 =108-
=108-
当且仅当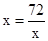 即
即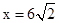 时取等号,∴△ADP面积的最大值为
时取等号,∴△ADP面积的最大值为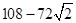 ,此时
,此时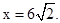
考点:本题主要考查函数模型,应用导数研究函数的最值,均值定理的应用。
点评:中档题,利通过分析图形特征,构建函数模型,再利用导数研究函数的最值,后利用均值定理确定函数的最值,从而解决实际问题。属于常见题目。本解法应用均值定理求函数的最值,应注意“一正,二定,三相等”缺一不可。

练习册系列答案
相关题目
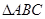 中,角
中,角 所对的边分别为
所对的边分别为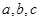 ,且满足
,且满足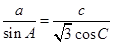 .
. 的大小;
的大小;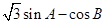 的最大值,并求此时角
的最大值,并求此时角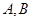 的大小.
的大小.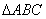 中,内角A,B,C的对边分别为
中,内角A,B,C的对边分别为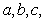 且
且 ,b=2,求A的值。
,b=2,求A的值。 中,边
中,边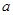 、
、 、
、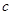 分别是角
分别是角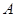 、
、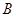 、
、 的对边,且满足
的对边,且满足 .
.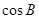 ;
;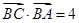 ,
,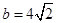 ,求边
,求边 中,内角
中,内角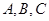 的对边分别为
的对边分别为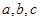 .
.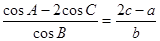 .
.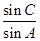 的值;
的值;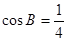 ,
,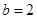 ,求
,求 的面积.
的面积. 中,角
中,角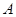 、
、 、
、 的对边分别为
的对边分别为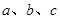 ,且满足
,且满足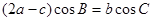 ,
, 、求角
、求角 、若
、若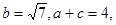 求
求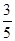 .
.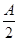 -cos(B+C)的值;
-cos(B+C)的值;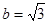 , B=
, B=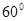 ,
, =1,求
=1,求 和A、C.
和A、C.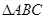 中,
中,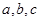 分别是内角
分别是内角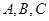 所对边长,且
所对边长,且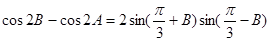 .
.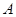 的大小;
的大小;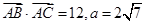 ,求
,求 .
.