题目内容
 在如图所示的空间直角坐标系O-xyz中,原点O是BC的中点,A点坐标为(
在如图所示的空间直角坐标系O-xyz中,原点O是BC的中点,A点坐标为(
| ||
| 2 |
| 1 |
| 2 |
(Ⅰ)求D点坐标;
(Ⅱ)求cos<
| AD, |
| BC |
分析:(Ⅰ)在平面yoz上,通过解直角三角形即可求得D点的坐标;
(Ⅱ)由已知A点的坐标及(Ⅰ)中求得的D的坐标,得到向量
的坐标,求出向量
的坐标,然后由向量的夹角公式求解.
(Ⅱ)由已知A点的坐标及(Ⅰ)中求得的D的坐标,得到向量
| AD |
| BC |
解答:解:(Ⅰ)如图,
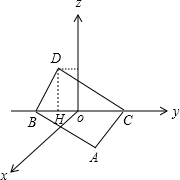
在平面yoz上,过D点作DH⊥BC,垂足为H.
在△BDC中,由∠BDC=90°,∠DCB=30°,BC=2,
得BD=
BC=1,DH=BDsin∠DBH=1×
=
,BH=
BD=
,OH=
,
∴D点坐标为(0,-
,
);
(Ⅱ)由A(
,
,0), D(0,-
,
),得
=(-
,-1,
),
由题设知:B(0,-1,0),C(0,1,0),
∴
=(0,2,0),
•
=(-
,-1,
)•(0,2,0)=-2,
|
|=
=
,|
=2|,
∴cos<
,
> =
=
=-
.

在平面yoz上,过D点作DH⊥BC,垂足为H.
在△BDC中,由∠BDC=90°,∠DCB=30°,BC=2,
得BD=
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴D点坐标为(0,-
| 1 |
| 2 |
| ||
| 2 |
(Ⅱ)由A(
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| AD |
| ||
| 2 |
| ||
| 2 |
由题设知:B(0,-1,0),C(0,1,0),
∴
| BC |
| AD |
| BC |
| ||
| 2 |
| ||
| 2 |
|
| AD |
(-
|
| ||
| 2 |
| BC |
∴cos<
| AD |
| BC |
| ||||
|
|
| -2 | ||||
|
| ||
| 5 |
点评:本题考查了空间中点的坐标的求解,考查了利用空间向量求异面直线所成的角,考查了学生的计算能力,是中档题.

练习册系列答案
 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案
相关题目
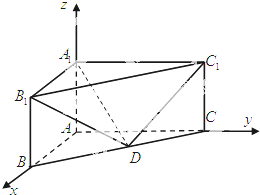 三棱柱ABC-A1B1C1在如图所示的空间直角坐标系中,已知AB=2,AC=4,AA1=3.D是BC的中点.
三棱柱ABC-A1B1C1在如图所示的空间直角坐标系中,已知AB=2,AC=4,AA1=3.D是BC的中点. 在如图所示的空间直角坐标系中,AB=AD=2,AC=4,E,F分别是AD,BD的中点.
在如图所示的空间直角坐标系中,AB=AD=2,AC=4,E,F分别是AD,BD的中点. ,D点在平面yoz上,BC=2,∠BDC=90°,∠DCB=30°.
,D点在平面yoz上,BC=2,∠BDC=90°,∠DCB=30°.
 的值.
的值.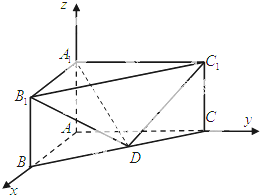 三棱柱ABC-A1B1C1在如图所示的空间直角坐标系中,已知AB=2,AC=4,AA1=3.D是BC的中点.
三棱柱ABC-A1B1C1在如图所示的空间直角坐标系中,已知AB=2,AC=4,AA1=3.D是BC的中点.