题目内容
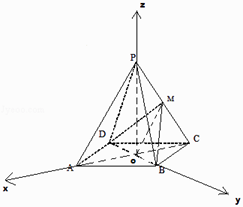
【题目】已知四棱锥P﹣ABCD中底面四边形ABCD是正方形,各侧面都是边长为2的正三角形,M是棱PC的中点.建立空间直角坐标系,利用空间向量方法解答以下问题: 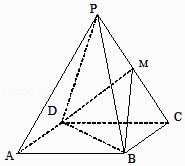
(1)求证:PA∥平面BMD;
(2)求二面角M﹣BD﹣C的平面角的大小.
【答案】
(1)证明:连结AC、BD交于点O,连结OP.
∵四边形ABCD是正方形,∴AC⊥BD∵PA=PC,∴OP⊥AC,
同理OP⊥BD,
以O为原点, ![]() 分别为x,y,z轴的正方向,建立空间直角坐标系O﹣xyz,
分别为x,y,z轴的正方向,建立空间直角坐标系O﹣xyz,
![]() ,
,
![]() ,
,
平面BMD的法向量为 ![]() ,
,
∵ ![]() ,
, ![]() ,又PA平面BMD,
,又PA平面BMD,
∴PA∥平面BMD
(2)解:平面ABCD的法向量为 ![]()
平面MBD的法向量为 ![]() ,
,
则 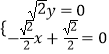 ,即
,即 ![]() ,
,
∴ ![]() …(9分)
…(9分)
二面角M﹣BD﹣C的平面角为α,
则 ![]() ,α=45°
,α=45°
∴二面角M﹣BD﹣C的平面角45°
【解析】(1)连结AC、BD交于点O,连结OP,以O为原点, ![]() 分别为x,y,z轴的正方向,建立空间直角坐标系O﹣xyz,利用向量法能证明PA∥平面BMD.(2)求出平面ABCD的法向量和平面MBD的法向量,利用向量法能求出二面角M﹣BD﹣C的平面角.
分别为x,y,z轴的正方向,建立空间直角坐标系O﹣xyz,利用向量法能证明PA∥平面BMD.(2)求出平面ABCD的法向量和平面MBD的法向量,利用向量法能求出二面角M﹣BD﹣C的平面角.
【考点精析】解答此题的关键在于理解直线与平面平行的判定的相关知识,掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目