题目内容
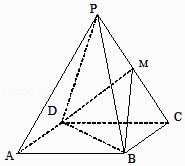
【题目】在梯形ABCD中,AD∥BC,∠ABC=90°,点M、N分别在边AB、BC上,沿直线MD、DN、NM,分别将△AMD、△CDN、△BNM折起,点A,B,C重合于一点P. 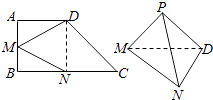
(1)证明:平面PMD⊥平面PND;
(2)若cos∠DNP= ![]() ,PD=5,求直线PD与平面DMN所成角的正弦值.
,PD=5,求直线PD与平面DMN所成角的正弦值.
【答案】
(1)证明:∵翻折前MB⊥NB,MA⊥DA,∴翻折后MP⊥NP,MP⊥PD,
∵NP∩PD=P,∴MP⊥平面PND,
∵MP平面PMD,∴平面PMD⊥平面PND
(2)解:由题意得AM=BM=PM,BN=CN=PN,AD=CD=PN,
设AM=a,BN=b,作DH⊥BC,NH= ![]() ,
,
∴AD=BN+NH=b+ ![]() ,
,
∴ ![]() =3ab+
=3ab+ ![]() ,
,
S△MND=S梯形ABCD﹣S△AMD﹣S△MBN﹣S△DNC
=3ab+ ![]() ﹣
﹣ ![]()
=ab+ ![]() ,
,
![]() =
= ![]() =
= ![]() =
= ![]() .
.
PO⊥平面MPN,
PO= ![]() =
= ![]() =
= ![]() ,
,
sin ![]() ,
,
如图,  ,
,
解得a= ![]() ,b=
,b= ![]() ,代入上式得sin∠PDO=
,代入上式得sin∠PDO= ![]() .
.
∴直线PD与平面DMN所成角的正弦值为 ![]() .
.

【解析】(1)推导出翻折后MP⊥NP,MP⊥PD,由此能证明平面PMD⊥平面PND.(2)由题意得AM=BM=PM,BN=CN=PN,AD=CD=PN,设AM=a,BN=b,作DH⊥BC,由此入手能求出直线PD与平面DMN所成角的正弦值.
【考点精析】根据题目的已知条件,利用平面与平面垂直的判定和空间角的异面直线所成的角的相关知识可以得到问题的答案,需要掌握一个平面过另一个平面的垂线,则这两个平面垂直;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则 .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目