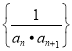Question

【题目】（本小题满分13分）设关于的一元二次方程 （）有两根和，且满足．

（1）试用表示；

（2）求证：数列是等比数列；

（3）当时，求数列的通项公式，并求数列的前项和．

Answer 1

【答案】（1）；（2）详见解析；（3）

【解析】

试题分析：（1）由韦达定理可得，，代入已知和关系式可得与的关系式．（2）由（1）中所得的与的关系式，根据等比数列的定义证为常数．（3）根据等比数列的通项公式可先求得，从而可得．根据分组求和及错位相减法可求得数列的前项和．

试题解析：解：（1）根据韦达定理，得，，

由

得 ，故

（2）证明：，

若，则，从而，

这时一元二次方程无实数根，故，

所以，数列是公比为的等比数列．

（3）设，则数列是公比的等比数列，

又，

所以，

所以，．

则由错位相减法可得．