题目内容
14．用数学归纳法证明2+3+4+…+n=$\frac{（n-1）（n+2）}{2}$时，第一步取n=2．分析 利用数学归纳法证明的步骤即可得出．
解答 解：利用数学归纳法证明2+3+4+…+n=$\frac{（n-1）（n+2）}{2}$时，第一步取n=2，左边=2，右边=$\frac{（2-1）×（2+2）}{2}$=2，因此左边=右边．
故答案为：2．
点评 本题考查了数学归纳法证明的步骤，考查了推理能力，属于基础题．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
4．已知函数f（x）=$\frac{{x}^{2}+x+1}{{x}^{2}+1}$，若f（a）=$\frac{4}{3}$，则f（-a）=（ ）
| A． | $\frac{2}{3}$ | B． | -$\frac{2}{3}$ | C． | $\frac{4}{3}$ | D． | -$\frac{4}{3}$ |
5．若直线y=x+b与曲线x2-4x+y2-6y+9=0（y≤3）有公共点，则b的取值范围是（ ）
| A． | [-1，1+2$\sqrt{2}$] | B． | [1-2$\sqrt{2}$，1+2$\sqrt{2}$] | C． | [1-2$\sqrt{2}$，3] | D． | [1-$\sqrt{2}$，3] |
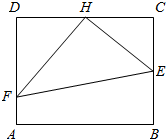某高校专家楼前现有一块矩形草坪ABCD，已知草坪长AB=100米，宽BC=50$\sqrt{3}$米，为了便于专家平时工作、起居，该高校计划在这块草坪内铺设三条小路HE、HF和EF，并要求H是CD的中点，点E在边BC上，点F在边AD上，且∠EHF为直角，如图所示．