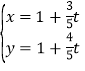题目内容
【题目】己知p:函数f(x)在R上是增函数,f(m2)<f(m+2)成立;q:方程![]() 1(m∈R)表示双曲线.
1(m∈R)表示双曲线.
(1)若p为真命题,求m的取值范围;
(2)若p∨q为真,p∧q为假,求m的取值范围.
【答案】(1) ﹣1<m<2.(2) (﹣1,0]∪[2,3).
【解析】
(1)根据增函数的定义即可求出m的取值范围
(2)由p∨q为真,p∧q为假可得有两种情况:①p真q假,②p假q真
(1)己知命题p:函数f(x)在R上是增函数,f(m2)<f(m+2)成立;
所以m2<m+2,解得﹣1<m<2.
(2)已知命题q:方程![]() 1(m∈R)表示双曲线.
1(m∈R)表示双曲线.
所以m(m﹣3)<0,解得0<m<3.
由于p∨q为真,p∧q为假,
所以①p真q假,则![]() ,解得﹣1<m≤0.
,解得﹣1<m≤0.
②p假q真,则 ,解得2≤m<3,
,解得2≤m<3,
综上所述:m的取值范围是(﹣1,0]∪[2,3).

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目