题目内容
【题目】已知曲线C：x2－y2＝1及直线l：y＝kx－1.
(1)若l与C有两个不同的交点，求实数k的取值范围；
(2)若l与C交于A，B两点，O为坐标原点，且△AOB的面积为
，求实数k的值．
【答案】（1）(－
，－1)∪(－1,1)∪(1，)（2）k＝0或k＝±
.
【解析】
(1)由
消去y，得(1－k2)x2＋2kx－2＝0.再解不等式组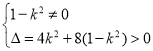
即得解.(2)先写出韦达定理，再求出S△OAB＝S△OAD＋S△OBD＝
|x1|＋|x2|＝|x1－x2|＝，再把韦达定理代入即得实数k的值.
(1)由消去y，得(1－k2)x2＋2kx－2＝0.
由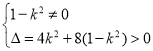得k的取值范围是(－，－1)∪(－1,1)∪(1，)．
(2)设点A(x1，y1)，B(x2，y2)．
由(1)，得x1＋x2＝－
，x1x2＝－
.
又∵l过点D(0，－1)，
∴S△OAB＝S△OAD＋S△OBD＝|x1|＋|x2|＝|x1－x2|＝,
∴(x1－x2)2＝(2)2，即
，
解得k＝0或k＝±
.
【题目】一只红铃虫的产卵数
和温度
有关，现收集了6组观测数据如下表：
温度 | 21 | 24 | 25 | 27 | 29 | 32 |
产卵数 | 7 | 11 | 21 | 24 | 66 | 115 |
| 1.946 | 2.398 | 3.045 | 3.178 | 4.191 | 4.745 |
（I）以温度为23、25、27、29的数据分别建立：①和之间线性回归方程
，②
和之间线性回归方程
；
（Ⅱ）若以（Ⅰ）所得回归方程预测，得到温度为21、32的数据如下：
温度 | 21 | 32 |
| -11.5 | 80.94 |
| 1.825 | 4.857 |
试以上表数据说明①②两个模型，哪个拟合的效果更好.
参考数据：
【题目】某省级示范高中高三年级对考试的评价指标中，有“难度系数”“区分度”和“综合”三个指标，其中，难度系数
，区分度
，综合指标
．以下是高三年级 6 次考试的统计数据：
i | 1 | 2 | 3 | 4 | 5 | 6 |
难度系数 xi | 0.66 | 0.72 | 0.73 | 0.77 | 0.78 | 0.84 |
区分度 yi | 0.19 | 0.24 | 0.23 | 0.23 | 0.21 | 0.16 |
(I) 计算相关系数
，若
，则认为
与
的相关性强；通过计算相关系数 ，能否认为与的相关性很强(结果保留两位小数)?
(II) 根据经验，当
时，区分度与难度系数的相关性较强，从以上数据中剔除(0.7,0.8)以外的 值，即
．
(i) 写出剩下 4 组数据的线性回归方程(
保留两位小数)；
(ii) 假设当时， 与的关系依从(i)中的回归方程，当 为何值时，综合指标
的值最大？
参考数据：
参考公式：
相关系数
回归方程中斜率和截距的最小二乘估计公式为
