题目内容
【题目】已知正四面体![]() 的表面积为
的表面积为![]() ,
,![]() 为棱
为棱![]() 的中点,球
的中点,球![]() 为该正四面体的外接球,则过点
为该正四面体的外接球,则过点![]() 的平面被球
的平面被球![]() 所截得的截面面积的最小值为( )
所截得的截面面积的最小值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
本题首先可以将正四面体放入正方体中,然后借助正方体的性质得出外接球的球心,通过正四面体![]() 的表面积为
的表面积为![]() 即可计算出
即可计算出![]() 长,从而求得外接球的半径
长,从而求得外接球的半径![]() ,利用截面圆的性质求得最小截面圆的半径径,问题得解。
,利用截面圆的性质求得最小截面圆的半径径,问题得解。
如图所示,
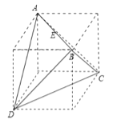
将正四面体放入正方体中,则正方体的中心即为其外接球的球心![]() ,
,
因为正四面体![]() 的表面积为
的表面积为![]() ,
,
所以![]() ,
,
因为![]() 是正三角形,所以
是正三角形,所以![]() ,
,![]() ,
,
设正方体的边长为![]() ,则:
,则:![]() ,解得:
,解得:![]()
所以正四面体![]() 的外接球直径为
的外接球直径为![]() ,
,
设过点![]() 的截面圆半径为
的截面圆半径为![]() ,球心
,球心![]() 到截面圆的距离为
到截面圆的距离为![]() ,正四面体
,正四面体![]() 的外接球半径为
的外接球半径为![]() ,
,
由截面圆的性质可得:![]()
当![]() 最大时,
最大时,![]() 最小,此时对应截面圆的面积最小.
最小,此时对应截面圆的面积最小.
又![]() ,所以
,所以![]() 的最大值为
的最大值为![]() ,此时
,此时![]() 最小为
最小为![]()
所以过点![]() 的最小截面圆的面积为
的最小截面圆的面积为![]() ,故选B。
,故选B。

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目