题目内容
为适应新课改,切实减轻学生负担,提高学生综合素质,某市某学校高三年级文科生300人在数学选修4-4、4-5、4-7选课方面进行改革,由学生自由选择2门(不可多选或少选),选课情况如下表:| 4-4 | 4-5 | 4-7 | |
| 男生 | 130 | a | 80 |
| 女生 | b | 100 | 60 |
(2)为方便开课,学校要求a≥110,b>110,计算a>b的概率.
【答案】分析:(1)由分层抽样的特点可得 ,解之可得a,结合总人数可得b值;
,解之可得a,结合总人数可得b值;
(2)可列举出满足a≥110,b>110的基本事件,找出a>b的情况,代入概率公式可得.
解答:解:(1)由每生选2科知共有600人次选课,所以按分层抽样得: ,
,
解得a=116,从而可得b=114,
(2)因为a+b=230
a≥110,b>110,所以(a,b)的取值有:
(110,120)(111,119)(112,118)(113,117)
(114,116)(115,115)(116,114)(117,113)
(118,112)(119,111)共10种;
其中的情况有(116,114)(117,113)(118,112)(119,111)共4种;
所以a>b的概率为:p=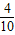 =
=
点评:本题考查古典概型的求解,涉及分层抽样的特点,属基础题.
 ,解之可得a,结合总人数可得b值;
,解之可得a,结合总人数可得b值;(2)可列举出满足a≥110,b>110的基本事件,找出a>b的情况,代入概率公式可得.
解答:解:(1)由每生选2科知共有600人次选课,所以按分层抽样得:
 ,
,解得a=116,从而可得b=114,
(2)因为a+b=230
a≥110,b>110,所以(a,b)的取值有:
(110,120)(111,119)(112,118)(113,117)
(114,116)(115,115)(116,114)(117,113)
(118,112)(119,111)共10种;
其中的情况有(116,114)(117,113)(118,112)(119,111)共4种;
所以a>b的概率为:p=
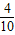 =
=
点评:本题考查古典概型的求解,涉及分层抽样的特点,属基础题.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
为适应新课改,切实减轻学生负担,提高学生综合素质,某市某学校高三年级文科生300人在数学选修4-4、4-5、4-7选课方面进行改革,由学生自由选择2门(不可多选或少选),选课情况如下表:
|
|
4-4 |
4-5 |
4-7 |
|
男生 |
130 |
|
80 |
|
女生 |
|
100 |
60 |
(1)为了解学生情况,现采用分层抽样方法抽取了三科作业共50本,统计发现4-5有18本,试根据这一数据求出 ,
, 的值.
的值.
(2)为方便开课,学校要求 ≥110,
≥110, >110,计算
>110,计算 >
> 的概率.
的概率.
(本小题满分12分)
为适应新课改,切实减轻学生负担,提高学生综合素质,怀化市某学校高三年级文科生300人在数学选修4-4、4-5、4-7选课方面进行改革,由学生自由选择2门(不可多选或少选),选课情况如下表:
| 4-4 | 4-5 | 4-7 | |
| 男生 | 130 |
| 80 |
| 女生 |
| 100 | 60 |
(1)为了解学生情况,现采用分层抽样方法抽取了三科作业共50本,统计发现4-5有18本,
试根据这一数据求出![]() ,
,![]() 的值。
的值。
(2)为方便开课,学校要求![]() ,
,![]() ,计算
,计算![]() 的概率。
的概率。