题目内容
【题目】已知椭圆C:![]() (
(![]() )的离心率为
)的离心率为![]() ,左、右焦点分别为
,左、右焦点分别为![]() ,
,![]() ,过
,过![]() 的直线与C交于M,N两点,
的直线与C交于M,N两点,![]() 的周长为
的周长为![]() .
.
(1)求椭圆C的标准方程;
(2)过M作与y轴垂直的直线l,点![]() ,试问直线
,试问直线![]() 与直线l交点的横坐标是否为定值?请说明理由.
与直线l交点的横坐标是否为定值?请说明理由.
【答案】(1)![]() ;(2)为定值2,理由见解析
;(2)为定值2,理由见解析
【解析】
(1)由离心率和过焦点的三角形的周长及a,b,c之间的关系求出a,b的值,进而求出椭圆的方程;
(2)由(1)可得直线![]() 的方程,与椭圆联立求出两根之和及两根之积,求出
的方程,与椭圆联立求出两根之和及两根之积,求出![]() 的方程令
的方程令![]() ,求出x的表达式,将两根之和及两根之积代入可得为定值2,
,求出x的表达式,将两根之和及两根之积代入可得为定值2,
解:(1)三角形![]() 的周长
的周长![]() ,
,![]() ,
,![]() ,可得:
,可得:![]() ,
,![]() ,
,
所以椭圆的方程为:![]() ;
;
(2)设![]() ,
,![]() ,
,
由(1)得![]() ,设直线
,设直线![]() 的直线为:
的直线为:![]() ,
,
联立直线与椭圆的方程: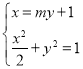 ,解得:
,解得:![]() ,
,
∴![]() ,
,![]() ,
,
直线![]() 的方程:
的方程: ,令
,令![]() ,可得:
,可得:
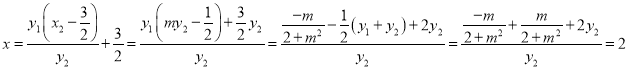 所以直线
所以直线![]() 与直线l交点的横坐标为定值2.
与直线l交点的横坐标为定值2.

练习册系列答案
相关题目
【题目】近年来,某市为了促进生活垃圾的分类处理,将生活垃圾分为厨余垃圾、可回收物和其他垃圾三类,并分别设置了相应的垃圾箱.为调查居民生活垃圾分类投放情况,现随机抽取了该市三类垃圾箱中总计1000吨生活垃圾,数据统计如下(单位:吨):
“厨余垃圾”箱 | “可回收物”箱 | “其他垃圾”箱 | |
厨余垃圾 | 400 | 100 | 100 |
可回收物 | 30 | 240 | 30 |
其他垃圾 | 20 | 20 | 60 |
(Ⅰ)试估计厨余垃圾投放正确的概率
(Ⅱ)试估计生活垃圾投放错误的概率
(Ⅲ)假设厨余垃圾在“厨余垃圾”箱、“可回收物”箱、“其他垃圾”箱的投放量分别为a,b,c,其中a>0,a+b+c=600.当数据a,b,c,的方差![]() 最大时,写出a,b,c的值(结论不要求证明),并求此时
最大时,写出a,b,c的值(结论不要求证明),并求此时![]() 的值.
的值.
(注:![]() ,其中
,其中![]() 为数据
为数据![]() 的平均数)
的平均数)