题目内容
【题目】设![]() 为正整数,区间
为正整数,区间![]() (其中
(其中![]() ,
,![]() )同时满足下列两个条件:
)同时满足下列两个条件:
①对任意![]() ,存在
,存在![]() 使得
使得![]() ;
;
②对任意![]() ,存在
,存在![]() ,使得
,使得![]() (其中
(其中![]() ).
).
(Ⅰ)判断![]() 能否等于
能否等于![]() 或
或![]() ;(结论不需要证明).
;(结论不需要证明).
(Ⅱ)求![]() 的最小值;
的最小值;
(Ⅲ)研究![]() 是否存在最大值,若存在,求出
是否存在最大值,若存在,求出![]() 的最大值;若不在在,说明理由.
的最大值;若不在在,说明理由.
【答案】(Ⅰ)![]() 可以等于
可以等于![]() ,但
,但![]() 不能等于
不能等于![]() ;(Ⅱ)
;(Ⅱ)![]() ;(Ⅲ)
;(Ⅲ)![]() 存在最大值,为
存在最大值,为![]() .
.
【解析】
(Ⅰ)根据题意可得出结论;
(Ⅱ)根据(Ⅰ)中的结论得出![]() 可以等于
可以等于![]() ,可得出区间
,可得出区间![]() 的长度为
的长度为![]() ,结合①得出
,结合①得出![]() ,再由
,再由![]() ,
,![]() ,
,![]() ,
,![]() 满足条件①、②可得出
满足条件①、②可得出![]() 的最小值;
的最小值;
(Ⅲ)利用反证法推导出![]() ,进而得出
,进而得出![]() ,由此得出
,由此得出![]() ,进而得出
,进而得出![]() ,再举例说明
,再举例说明![]() 成立,由此可得出正整数
成立,由此可得出正整数![]() 的最大值.
的最大值.
(Ⅰ)![]() 可以等于
可以等于![]() ,但
,但![]() 不能等于
不能等于![]() ;
;
(Ⅱ)记![]() 为区间
为区间![]() 的长度,则区间
的长度,则区间![]() 的长度为
的长度为![]() ,
,![]() 的长度为
的长度为![]() .
.
由①,得![]() .
.
又因为![]() ,
,![]() ,
,![]() ,
,![]() 显然满足条件①,②.
显然满足条件①,②.
所以![]() 的最小值为
的最小值为![]() ;
;
(Ⅲ)![]() 的最大值存在,且为
的最大值存在,且为![]() .
.
解答如下:(1)首先,证明![]() .
.
由②,得![]() 、
、![]() 、
、![]() 、
、![]() 互不相同,且对于任意
互不相同,且对于任意![]() ,
,![]() .
.
不妨设![]() .
.
如果![]() ,那么对于条件②,当
,那么对于条件②,当![]() 时,不存在
时,不存在![]() ,使得
,使得![]() .
.
这与题意不符,故![]() .
.
如果![]() ,那么
,那么![]() ,
,
这与条件②中“存在![]() ,使得
,使得![]() (其中
(其中![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() )”矛盾,故
)”矛盾,故![]() .
.
所以![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() .
.
故![]() .
.
若存在![]() ,这与条件②中“存在
,这与条件②中“存在![]() ,使得
,使得![]() ”矛盾,
”矛盾,
所以![]() .
.
(2)给出![]() 存在的例子 .
存在的例子 .
令![]() ,其中
,其中![]() 、
、![]() 、
、![]() 、
、![]() ,即
,即![]() 、
、![]() 、
、![]() 、
、![]() 为等差数列,公差
为等差数列,公差![]() .
.
由![]() ,知
,知![]() ,则易得
,则易得![]() ,
,
所以![]() 、
、![]() 、
、![]() 、
、![]() 满足条件①.
满足条件①.
又公差![]() ,
,
所以![]() ,
,![]() .(注:
.(注:![]()
为区间![]() 的中点对应的数)
的中点对应的数)
所以![]() 、
、![]() 、
、![]() 、
、![]() 满足条件②.
满足条件②.
综合(1)(2)可知![]() 的最大值存在,且为
的最大值存在,且为![]() .
.

【题目】微信运动,是由腾讯开发的一个类似计步数据库的公众账号.用户可以通过关注微信运动公众号查看自己每天行走的步数,同时也可以和其他用户进行运动量的![]() 或点赞.微信运动公众号为了解用户的一些情况,在微信运动用户中随机抽取了100名用户,统计了他们某一天的步数,数据整理如下:
或点赞.微信运动公众号为了解用户的一些情况,在微信运动用户中随机抽取了100名用户,统计了他们某一天的步数,数据整理如下:
|
|
|
|
|
|
|
| 5 | 20 | 50 | 15 | 5 | 5 |
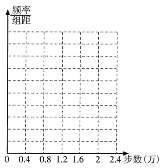
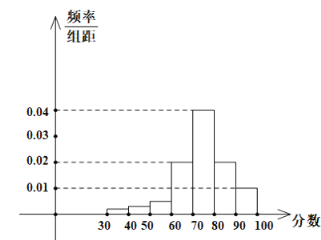
(1)根据表中数据,在如图所示的坐标平面中作出其频率分布直方图,并在纵轴上标明各小长方形的高;
(2)若视频率分布为概率分布,在微信运动用户中随机抽取3人,求至少2人步数多于1.2万步的概率;
(3)若视频率分布为概率分布,在微信运动用户中随机抽取2人,其中每日走路不超过0.8万步的有![]() 人,超过1.2万步的有
人,超过1.2万步的有![]() 人,设
人,设![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
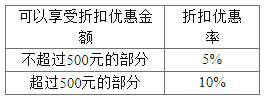
【题目】某险种的基本保费为a(单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下:
上年度出险次数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
保费 | 0.85a | a | 1.25a | 1.5a | 1.75a | 2a |
随机调查了该险种的200名续保人在一年内的出险情况,得到如下统计表:
出险次数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
频数 | 60 | 50 | 30 | 30 | 20 | 10 |
(1)记A为事件:“一续保人本年度的保费不高于基本保费”,求P(A)的估计值;
(2)记B为事件:“一续保人本年度的保费高于基本保费但不高于基本保费的160%”,求P(B)的估计值;
(3)求续保人本年度平均保费的估计值.