题目内容
已知函数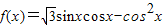 .
.(I)求f(x)的最小正周期和单调递增区间;
(II)当
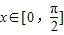 时,求函数f(x)的最大值和最小值及相应的x的值.
时,求函数f(x)的最大值和最小值及相应的x的值.
【答案】分析:(I)根据倍角公式及和差角公式,我们可以化简函数的解析式,进而根据正弦型函数的周期性和单调性,可求出f(x)的最小正周期和单调递增区间;
(II)当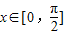 时,-
时,- ≤
≤ ≤
≤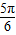 ,结合正弦函数的最值,可求出函数f(x)的最大值和最小值及相应的x的值.
,结合正弦函数的最值,可求出函数f(x)的最大值和最小值及相应的x的值.
解答:解:(I)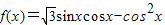 =
=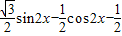 =
=
∵ω=2,
∴T=π,即f(x)的最小正周期为π
由2kπ-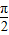 ≤
≤ ≤2kπ-
≤2kπ-
得kπ- ≤x≤kπ+
≤x≤kπ+
∴f(x)的单调递增区间为[kπ-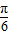 ,kπ+
,kπ+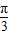 ](k∈Z)
](k∈Z)
(II)∵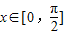
∴- ≤
≤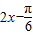 ≤
≤
当 =
= ,即x=
,即x= 时,f(x)的最大值为
时,f(x)的最大值为
当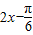 =-
=- ,即x=0时,f(x)的最小值为-1
,即x=0时,f(x)的最小值为-1
点评:本题考查的知识点是两角和与差的正弦函数,熟练掌握正弦型函数的周期性,单调性,最值等性质是解答的关键.
(II)当
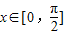 时,-
时,- ≤
≤ ≤
≤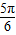 ,结合正弦函数的最值,可求出函数f(x)的最大值和最小值及相应的x的值.
,结合正弦函数的最值,可求出函数f(x)的最大值和最小值及相应的x的值.解答:解:(I)
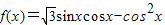 =
=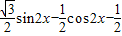 =
=
∵ω=2,
∴T=π,即f(x)的最小正周期为π
由2kπ-
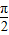 ≤
≤ ≤2kπ-
≤2kπ-
得kπ-
 ≤x≤kπ+
≤x≤kπ+
∴f(x)的单调递增区间为[kπ-
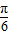 ,kπ+
,kπ+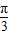 ](k∈Z)
](k∈Z)(II)∵
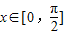
∴-
 ≤
≤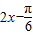 ≤
≤
当
 =
= ,即x=
,即x= 时,f(x)的最大值为
时,f(x)的最大值为
当
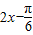 =-
=- ,即x=0时,f(x)的最小值为-1
,即x=0时,f(x)的最小值为-1点评:本题考查的知识点是两角和与差的正弦函数,熟练掌握正弦型函数的周期性,单调性,最值等性质是解答的关键.

练习册系列答案
相关题目
 .
. .
. .
. =(
=( ,0)平移得到函数g(x)的图象,求函数g(x)在区间[0,π]上的最大值和最小值.
,0)平移得到函数g(x)的图象,求函数g(x)在区间[0,π]上的最大值和最小值. .
. 成等差数列,且
成等差数列,且 =9,求a的值.
=9,求a的值. .
.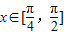 时,不等式|f(x)-m|<2恒成立,求实数m的取值范围.
时,不等式|f(x)-m|<2恒成立,求实数m的取值范围.