题目内容
已知函数 .
.(I)求f(x)的最小正周期与单调递增区间;
(II)若当
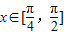 时,不等式|f(x)-m|<2恒成立,求实数m的取值范围.
时,不等式|f(x)-m|<2恒成立,求实数m的取值范围.
【答案】分析:(Ⅰ) 利用两角和差的余弦公式化简f(x)的解析式为cos(2x+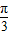 )+2,故周期为
)+2,故周期为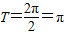 ,由
,由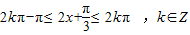 ,得到f(x)的单调递增区间.
,得到f(x)的单调递增区间.
(Ⅱ) 要使不等式恒成立,需m>f(x)max -2 且m<f(x)min +2,根据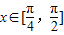 ,可求得f(x)的最大值和最小值,从而得到m的取值范围.
,可求得f(x)的最大值和最小值,从而得到m的取值范围.
解答:解:(Ⅰ)∵ ,
,
∴f(x)的最小正周期为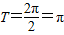 ,
,
由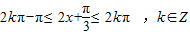 ,得
,得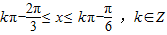 ,
,
∴f(x)的单调递增区间为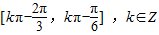 .
.
(Ⅱ)∵|f(x)-m|<2,f(x)-2<m<f(x)+2,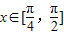 ,
,
∴m>f(x)max -2 且m<f(x)min +2,
又∵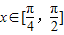 ,∴
,∴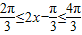 ,即
,即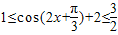 ,∴
,∴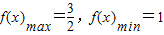 .
.
∴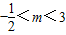 ,即m的取值范围是
,即m的取值范围是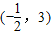 .
.
点评:本题考查两角和差的余弦公式的应用,余弦函数的单调性,周期性和最值,求出f(x)的解析式为cos(2x+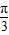 )+2,是解题的突破口.
)+2,是解题的突破口.
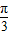 )+2,故周期为
)+2,故周期为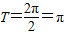 ,由
,由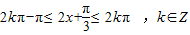 ,得到f(x)的单调递增区间.
,得到f(x)的单调递增区间.(Ⅱ) 要使不等式恒成立,需m>f(x)max -2 且m<f(x)min +2,根据
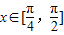 ,可求得f(x)的最大值和最小值,从而得到m的取值范围.
,可求得f(x)的最大值和最小值,从而得到m的取值范围.解答:解:(Ⅰ)∵
 ,
,∴f(x)的最小正周期为
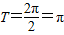 ,
,由
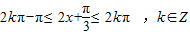 ,得
,得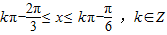 ,
,∴f(x)的单调递增区间为
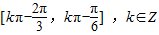 .
.(Ⅱ)∵|f(x)-m|<2,f(x)-2<m<f(x)+2,
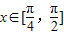 ,
,∴m>f(x)max -2 且m<f(x)min +2,
又∵
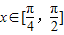 ,∴
,∴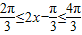 ,即
,即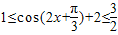 ,∴
,∴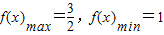 .
.∴
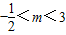 ,即m的取值范围是
,即m的取值范围是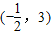 .
.点评:本题考查两角和差的余弦公式的应用,余弦函数的单调性,周期性和最值,求出f(x)的解析式为cos(2x+
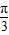 )+2,是解题的突破口.
)+2,是解题的突破口. 
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 .
. .
. .
. =(
=( ,0)平移得到函数g(x)的图象,求函数g(x)在区间[0,π]上的最大值和最小值.
,0)平移得到函数g(x)的图象,求函数g(x)在区间[0,π]上的最大值和最小值. .
. 成等差数列,且
成等差数列,且 =9,求a的值.
=9,求a的值.