题目内容
设![]() ,
, ![]() ,
, .
.
(1)若![]() , 且对任意实数
, 且对任意实数![]() 均有
均有![]() 成立, 求
成立, 求![]() 的表达式;
的表达式;
(2)在(1)的条件下, 若![]() 不是[-2, 2]上的单调函数, 求实数
不是[-2, 2]上的单调函数, 求实数![]() 的取值范围;
的取值范围;
解析:由f(0)=1得c=1
(1)由f(-2)=0得4a-2b+1=0, 又由f(x)≥0对x∈R恒成立, 知a>0且△=b2-4a c≤0
即b2-2b+1=(b-1)2≤0 ∴b=1, a=![]() 从而f(x)=
从而f(x)=![]() x2+x+1∴g(x)=
x2+x+1∴g(x)=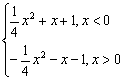
(2)由(1)知h(x)=![]() x2+(k+1) x+1, 其图象的对称轴为x= -2(k+1) ,
x2+(k+1) x+1, 其图象的对称轴为x= -2(k+1) ,
再由h(x)在 [-2, 2]上不是单调函数, 故得-2<-2(k+1)<2
解得-2<k<0
(3)当f(x)为偶函数时, f(-x)=f(x), ∴b=0, ∴f(x)=ax2+1, a>0
故f(x)在(0, +∞)上为增函数, 从而, g(x)在(0, +∞)上为减函数,
又m>0, n<0, m+n>0 ∴ m>-n>0, 从而g(m)<g(-n)
且g(-n)= -f(-n)= -f(n)= - g(n) 故得g(m)< -g(n), 因此, g(m)+g(n)<0
练习册系列答案
相关题目

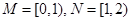 ,函数
,函数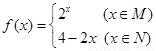 .
.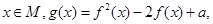 且
且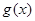 的最小值为1;求实数
的最小值为1;求实数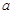 的值
的值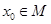 ,且
,且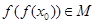 ,求
,求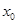 的取值范围.
的取值范围.