Question

【题目】如图，圆锥顶点为P，底面圆心为O，其母线与底面所成的角为22.5°，AB和CD是底面圆O上的两条平行的弦，轴OP与平面PCD所成的角为60°，

（1）证明：平面PAB与平面PCD的交线平行于底面；
（2）求cos∠COD．

Answer 1

【答案】
（1）证明：设平面PAB与平面PCD的交线为l，则

∵AB∥CD，AB平面PCD，∴AB∥平面PCD

∵AB面PAB，平面PAB与平面PCD的交线为l，∴AB∥l

∵AB在底面上，l在底面外

∴l与底面平行；

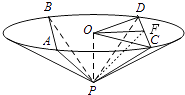
（2）解：设CD的中点为F，连接OF，PF

由圆的性质，∠COD=2∠COF，OF⊥CD

∵OP⊥底面，CD底面，∴OP⊥CD

∵OP∩OF=O

∴CD⊥平面OPF

∵CD平面PCD

∴平面OPF⊥平面PCD

∴直线OP在平面PCD上的射影为直线PF

∴∠OPF为OP与平面PCD所成的角

由题设，∠OPF=60°

设OP=h，则OF=OPtan∠OPF=

∵∠OCP=22.5°，∴

∵tan45°= =1

∴tan22.5°=

∴OC= =

在Rt△OCF中，cos∠COF= = =

∴cos∠COD=cos（2∠COF）=2cos2∠COF﹣1=17﹣12

【解析】（1）利用线面平行的判定与性质，可证平面PAB与平面PCD的交线平行于底面；（2）先作出OP与平面PCD所成的角，再求出OC，OF，求出cos∠COF，利用二倍角公式，即可求得cos∠COD．
【考点精析】解答此题的关键在于理解空间中直线与直线之间的位置关系的相关知识，掌握相交直线：同一平面内，有且只有一个公共点；平行直线：同一平面内，没有公共点；异面直线： 不同在任何一个平面内，没有公共点，以及对空间中直线与平面之间的位置关系的理解，了解直线在平面内—有无数个公共点；直线与平面相交—有且只有一个公共点；直线在平面平行—没有公共点．