题目内容
 如图,椭圆
如图,椭圆| x2 |
| a2 |
| y2 |
| b |
| ||
| 2 |
(Ⅰ)求椭圆方程;
(Ⅱ)设F1、F2分别为椭圆的左、右焦点,求证:|AT|2=
| 1 |
| 2 |
分析:(Ⅰ)先写出过A、B的直线方程,因为由题意得
有惟一解.消去y得:(b2+
a2)x2-a2x+a2b2=0有惟一解,
利用其根的判别式等于0,即可求得a,b的值,从而得到椭圆方程;
(Ⅱ)由(Ⅰ)得c=
,所以F1(-
,0),F2(
,0)由
解得x1=x2=1,接下来利用距离公式求得线段的长,从而证得|AT|2=
|AF1|•|AF2|.
|
| 1 |
| 4 |
利用其根的判别式等于0,即可求得a,b的值,从而得到椭圆方程;
(Ⅱ)由(Ⅰ)得c=
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
|
| 1 |
| 2 |
解答:解:(Ⅰ)过A、B的直线方程为
+y=1
因为由题意得
有惟一解.
即(b2+
a2)x2-a2x+a2b2=0有惟一解,
所以△=a2b2(a2+4b2-4)=0(ab≠0),,
故(a2+4b2-4)=0
又因为c=
,即
=
,
所以a2=4b2
从而得a2=2,b2=
,
故所求的椭圆方程为
+2y2=1.
(Ⅱ)由(Ⅰ)得c=
,
所以F1(-
,0),F2(
,0)
由
解得x1=x2=1,,
因此T=(1,
).
从而|AT|2=
,
因为|AF1|•|AF2|=
,
所以|AT|2=
|AF1|•|AF2|
| x |
| 2 |
因为由题意得
|
即(b2+
| 1 |
| 4 |
所以△=a2b2(a2+4b2-4)=0(ab≠0),,
故(a2+4b2-4)=0
又因为c=
| ||
| 2 |
| a2-b2 |
| a2 |
| 3 |
| 4 |
所以a2=4b2
从而得a2=2,b2=
| 1 |
| 2 |
故所求的椭圆方程为
| x2 |
| 2 |
(Ⅱ)由(Ⅰ)得c=
| ||
| 2 |
所以F1(-
| ||
| 2 |
| ||
| 2 |
由
|
因此T=(1,
| 1 |
| 2 |
从而|AT|2=
| 5 |
| 4 |
因为|AF1|•|AF2|=
| 5 |
| 2 |
所以|AT|2=
| 1 |
| 2 |
点评:本小题主要考查直线与圆锥曲线的综合问题、直线方程、椭圆方程等基础知识,考查运算求解能力、方程思想.属于中档题.

练习册系列答案
相关题目
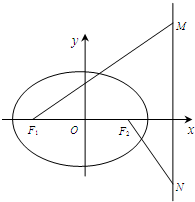 如图,椭圆
如图,椭圆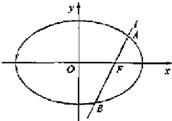 如图,椭圆
如图,椭圆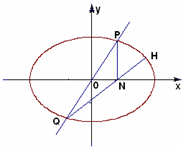 如图,椭圆
如图,椭圆 (2010•武清区一模)如图,椭圆
(2010•武清区一模)如图,椭圆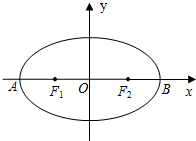 如图,椭圆
如图,椭圆