题目内容
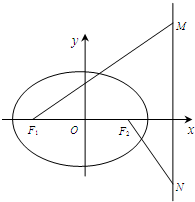 如图,椭圆
如图,椭圆| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 2 |
| 1 |
| 2 |
| F1M |
| F2N |
(1)求椭圆的方程;
(2)求MN的最小值;
(3)以MN为直径的圆C是否过定点?请证明你的结论.
分析:(1)因为:e=
=
,且过点P(1,
),列出关于a,b的方程,解得a,b.最后写出椭圆方程即可;
(2)设点M(4,y1),N(4,y2)写出向量的坐标,利用向量的数量积得到y1y2=-15,又MN=|y2-y1|=|-
-y1|=
+|y1|≥2
,结合基本不等式即可求得MN的最小值;
(3)利用圆心C的坐标和半径得出圆C的方程,再令y=0,得x2-8x+1=0从而得出圆C过定点.
| c |
| a |
| 1 |
| 2 |
| 3 |
| 2 |
(2)设点M(4,y1),N(4,y2)写出向量的坐标,利用向量的数量积得到y1y2=-15,又MN=|y2-y1|=|-
| 15 |
| y1 |
| 15 |
| |y1| |
| 15 |
(3)利用圆心C的坐标和半径得出圆C的方程,再令y=0,得x2-8x+1=0从而得出圆C过定点.
解答:解:(1)∵e=
=
,且过点P(1,
),
∴
解得
∴椭圆方程为
+
=1.(4分)
(2)设点M(4,y1),N(4,y2)则
=(5,y1),
=(3,y2),
•
=15+y1y2=0,
∴y1y2=-15,
又∵MN=|y2-y1|=|-
-y1|=
+|y1|≥2
,
∴MN的最小值为2
.
(3)圆心C的坐标为(4,
),半径r=
.
圆C的方程为(x-4)2+(y-
)2=
,
整理得:x2+y2-8x-(y1+y2)y+16+y1y2=0.∵y1y2=-15,∴x2+y2-8x-(y1+y2)y+1=0
令y=0,得x2-8x+1=0,∴x=4±
.∴圆C过定点(4±
,0).
| c |
| a |
| 1 |
| 2 |
| 3 |
| 2 |
∴
|
|
∴椭圆方程为
| x2 |
| 4 |
| y2 |
| 3 |
(2)设点M(4,y1),N(4,y2)则
| F1M |
| F2N |
| F1M |
| F2N |
∴y1y2=-15,
又∵MN=|y2-y1|=|-
| 15 |
| y1 |
| 15 |
| |y1| |
| 15 |
∴MN的最小值为2
| 15 |
(3)圆心C的坐标为(4,
| y1+y2 |
| 2 |
| |y2-y1| |
| 2 |
圆C的方程为(x-4)2+(y-
| y1+y2 |
| 2 |
| (y2-y1)2 |
| 4 |
整理得:x2+y2-8x-(y1+y2)y+16+y1y2=0.∵y1y2=-15,∴x2+y2-8x-(y1+y2)y+1=0
令y=0,得x2-8x+1=0,∴x=4±
| 15 |
| 15 |
点评:本小题主要考查椭圆的简单性质、圆与圆锥曲线的综合等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.

练习册系列答案
相关题目
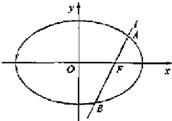 如图,椭圆
如图,椭圆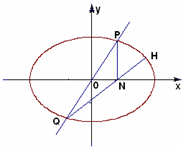 如图,椭圆
如图,椭圆 (2010•武清区一模)如图,椭圆
(2010•武清区一模)如图,椭圆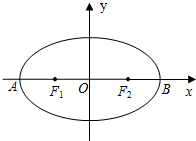 如图,椭圆
如图,椭圆