Question

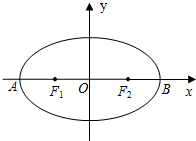如图，椭圆

x2

a2

+

y2

b2

=1（a＞b＞0）的左、右顶点分别是A，B，左、右焦点分别是F₁，F₂，若|AF₁|，|F₁F₂|，|F₁B|成等比数列，则此椭圆的离心率为（　　）

• A、

  1

  4

• B、

  1

  2

• C、

  5

  5

• D、

  5

  -2

Answer 1

分析：直接利用椭圆的定义，结合|AF₁|，|F₁F₂|，|F₁B|成等比数列，即可求出椭圆的离心率．故选C．

解答：解：∵椭圆

x2

a2

+

y2

b2

=1，（a＞b＞0）的左、右顶点分别是A，B，左、右焦点分别是F₁，F₂
设椭圆的半焦距为c，
则|AF₁|=a-c，|F₁F₂|=2c，|F₁B|=a+c，
∵|AF₁|，|F₁F₂|，|F₁B|成等比数列，
∴（a-c）（a+c）=4c²，
即a²=5c²，
∴e=

5

5

．
故选C．

点评：本题考查椭圆的基本性质的应用，离心率的求法，考查计算能力．