题目内容
11.设函数f(x)=$\left\{\begin{array}{l}{{2}^{-x},x<1}\\{lo{g}_{2}x,x≥1}\end{array}\right.$,则满足f(x)=$\frac{1}{4}$的x的值是${2}^{\frac{1}{4}}$.分析 利用分段函数列出方程,然后求解即可.
解答 解:函数f(x)=$\left\{\begin{array}{l}{{2}^{-x},x<1}\\{lo{g}_{2}x,x≥1}\end{array}\right.$,则满足f(x)=$\frac{1}{4}$,
可得x<1时,2-x=$\frac{1}{4}$,解得x=2舍去.
x≥1时,${log}_{2}x=\frac{1}{4}$,解得x=${2}^{\frac{1}{4}}$.
故答案为:${2}^{\frac{1}{4}}$.
点评 本题考查函数值的求法,分段函数的应用,考查计算能力.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
1.动圆M经过点A(3,0)且与直线l:x=-3相切,则动圆圆心M的轨迹方程是( )
| A. | y2=12x | B. | y2=6x | C. | y2=3x | D. | y2=24x |
6.某园林局对1 000株树木的生长情况进行调查,其中杉树600株,槐树400株.现用分层抽样方法从这1 000株树木中随机抽取100株,杉树与槐树的树干周长(单位:cm)的抽查结果如表:
(1)求x,y值;
(2)树干周长在30cm到40cm之间的4株槐树有1株患虫害,现要对这4株树逐一进行排查直至找出患虫害的树木为止,求排查的树木恰好为2株的概率.
| 树干周长(单位:cm) | [30,40) | [40,50) | [50,60) | [60,70) |
| 杉树 | 6 | 19 | 21 | x |
| 槐树 | 4 | 20 | y | 6 |
(2)树干周长在30cm到40cm之间的4株槐树有1株患虫害,现要对这4株树逐一进行排查直至找出患虫害的树木为止,求排查的树木恰好为2株的概率.
16.已知f(x)是定义在R上的奇函数,且当x<0时,f(x)=2x,则f(log49)的值为( )
| A. | -3 | B. | -$\frac{1}{3}$ | C. | $\frac{1}{3}$ | D. | 3 |
3.直线xsinα+y+2=0的倾斜角的取值范围是( )
| A. | [0,π) | B. | [0,$\frac{π}{4}$]∪[$\frac{3}{4}$π,π) | C. | [0,$\frac{π}{4}$] | D. | [0,$\frac{π}{4}$]∪($\frac{π}{2}$,π) |
20.下列三视图所对应的直观图是( )
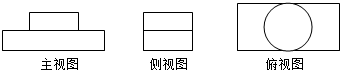

| A. |  | B. | 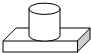 | C. | 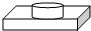 | D. | 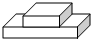 |
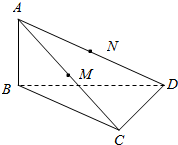 如图所示,已知AB⊥平面BCD,M、N分别是AC、AD的中点,BC⊥CD.
如图所示,已知AB⊥平面BCD,M、N分别是AC、AD的中点,BC⊥CD.