题目内容
16．已知f（x）是定义在R上的奇函数，且当x＜0时，f（x）=2x，则f（log49）的值为（ ）| A． | -3 | B． | -$\frac{1}{3}$ | C． | $\frac{1}{3}$ | D． | 3 |
分析 求出x＞0时，函数的解析式，即可得出结论．
解答 解：因为x＜0时，$f（x）=2_{\;}^x$，所以x＞0时，$f（-x）=-f（x）=2_{\;}^{-x}$，即$f（x）=-2_{\;}^{-x}$，
所以$f（{log_4}9）=f（{log_2}3）=-2_{\;}^{-{{log}_2}3}=-\frac{1}{3}$，
故选：B．
点评 本题考查函数的奇偶性，考查学生的计算能力，比较基础．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
7．F1是双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左焦点，点P是双曲线右支上一点，若线段PF1与y轴的交点M恰为PF1的中点，且|OM|=a（O为坐标原点），则C的离心率为（ ）
| A． | $\sqrt{2}$ | B． | $\sqrt{3}$ | C． | 2 | D． | 3 |
4．如图，设正方体ABCD-A1B1C1D1的棱长为1，则直线B1C与平面AB1D1所成的角的正弦值是（ ）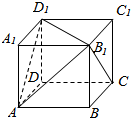
| A． | $\frac{2\sqrt{2}}{3}$ | B． | $\frac{\sqrt{3}}{6}$ | C． | $\frac{\sqrt{6}}{3}$ | D． | $\frac{\sqrt{2}}{3}$ |
8．满足{a，b}⊆A?{a，b，c，d，e}的集合A的个数是（ ）
| A． | 2 | B． | 6 | C． | 7 | D． | 8 |
6．已知α是第二象限角，tan（π+α）=-$\frac{8}{15}$，则cos（α-$\frac{π}{2}$）=（ ）
| A． | $\frac{1}{8}$ | B． | -$\frac{1}{8}$ | C． | $\frac{8}{17}$ | D． | -$\frac{8}{17}$ |