题目内容
已知椭圆C:![]() (a>b>0),点F1、F2分别是椭圆的左、右焦点,点P(2,
(a>b>0),点F1、F2分别是椭圆的左、右焦点,点P(2,![]() )在直线x=
)在直线x=![]() 上,且|F1F2|=|PF2|,直线
上,且|F1F2|=|PF2|,直线![]() :y=kx+m为动直线,且直线
:y=kx+m为动直线,且直线![]() 与椭圆C交于不同的两点A、B。
与椭圆C交于不同的两点A、B。
(Ⅰ)求椭圆C的方程;
(Ⅱ)若在椭圆C上存在点Q,满足![]() (O为坐标原点),求实数
(O为坐标原点),求实数![]() 的取值范围;
的取值范围;
(Ⅲ)在(Ⅱ)的条件下,当![]() 取何值时,△ABO的面积最大,并求出这个最大值.
取何值时,△ABO的面积最大,并求出这个最大值.
解:椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,
,
又![]() ,
,![]() ,
, ![]()
解得![]() ,
,
![]() 椭圆
椭圆![]() 的方程为
的方程为![]() .
.
(Ⅱ)由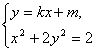 ,得
,得![]() .
.
设点![]() 、
、![]() 的坐标分别为
的坐标分别为![]() 、
、![]() ,则
,则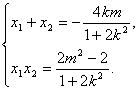
![]() .
.
(1)当![]() 时,点
时,点![]() 、
、![]() 关于原点对称,则
关于原点对称,则![]() .
.
(2)当![]() 时,点
时,点![]() 、
、![]() 不关于原点对称,则
不关于原点对称,则![]() ,
,
由![]() ,得
,得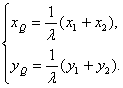 即
即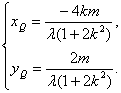
![]() 点
点![]() 在椭圆上,
在椭圆上,![]() 有
有![]() ,
,
化简,得![]() .
.
![]() ,
,![]() 有
有![]() .………………①
.………………①
又![]() ,
,
![]() 由
由![]() ,得
,得![]() .……………………………②
.……………………………②
将①、②两式,得![]() .
.
![]() ,
,![]() ,则
,则![]() 且
且![]() .
.
综合(1)、(2)两种情况,得实数![]() 的取值范围是
的取值范围是![]() .
.
(Ⅲ)![]() ,点
,点![]() 到直线
到直线![]() 的距离
的距离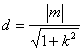 ,
,
![]() 的面积
的面积![]()
![]()
![]() .
.
由①有![]() ,代入上式并化简,得
,代入上式并化简,得![]() .
.
![]() ,
,![]() .
.
当且仅当![]() ,即
,即![]() 时,等号成立.
时,等号成立.
![]() 当
当![]() 时,
时,![]() 的面积最大,最大值为
的面积最大,最大值为![]() .
.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
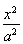









 (a>b>0)的离心率为
(a>b>0)的离心率为 ,短轴一个端点到右焦点的距离为3.
,短轴一个端点到右焦点的距离为3. (a>b>0)的离心率为
(a>b>0)的离心率为 短轴一个端点到右焦点的
短轴一个端点到右焦点的 .
. ,求△AOB面积的
,求△AOB面积的