Question

（本题满分14分）

已知椭圆C：(a＞b＞0)的离心率为,短轴一个端点到右焦点的距离为3.

(1)求椭圆C的方程;

(2)过椭圆C上的动点P引圆O：x²+y²=b²的两条切线PA、PB，A、B分别为切点，试探究椭圆C上是否存在点P，由点P向圆O所引的两条切线互相垂直？若存在，请求出点P的坐标；若不存在，请说明理由.

 

Answer 1

【答案】

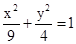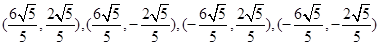 (1) .  (2)椭圆C上存在四个点，分别由这四个点向圆O所引的两条切线均互相垂直.  

【解析】本题主要考查圆与圆锥曲线的综合问题．解决第二问的关键在于根据条件分析出AOBP为正方形，|AO|=|AP|，得到关于点P坐标的等式．

（1）直接根据条件列出 a²=b²+c^2，a=3，e=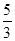，解方程求出b，c即可得到椭圆C的方程；

（2）先根据条件分析出AOBP为正方形，|AO|=|AP|，得到关于点P坐标的等式；再结合点P在椭圆上即可求出点P的坐标．

解：(1)设椭圆的半焦距为c,依题意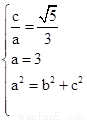,  ∴b=2,   ---------2分

∴所求椭圆方程为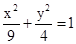.      ---------------4分

(2)如图，设P点坐标为(x₀,y₀),                -------5分

若∠APB=90°,则有|OA|=|AP|.               ---------6分

即|OA|=,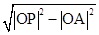

有2=,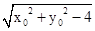

两边平方得x₀²+y₀²=8                       ①

又因为P(x₀,y₀)在椭圆上，所以4x₀²+9y₀²=36  ②

①,②联立解得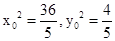            ---------9分

所以满足条件的有以下四组解

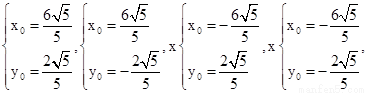     -----------12分

所以，椭圆C上存在四个点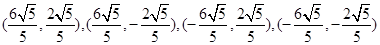，分别由这四个点向圆O所引的两条切线均互相垂直.         --------14分