题目内容
设函数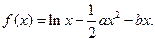
(Ⅰ)当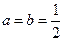 时,求
时,求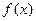 的最大值;
的最大值;
(Ⅱ)令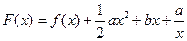 ,(
,(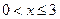 ),其图象上任意一点
),其图象上任意一点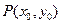 处切线的斜率
处切线的斜率 ≤
≤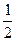 恒成立,求实数
恒成立,求实数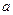 的取值范围;
的取值范围;
(Ⅲ)当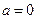 ,
,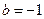 ,方程
,方程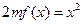 有唯一实数解,求正数
有唯一实数解,求正数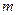 的值.
的值.
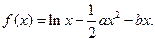
(Ⅰ)当
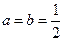 时,求
时,求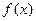 的最大值;
的最大值;(Ⅱ)令
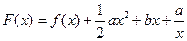 ,(
,(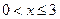 ),其图象上任意一点
),其图象上任意一点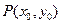 处切线的斜率
处切线的斜率 ≤
≤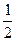 恒成立,求实数
恒成立,求实数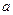 的取值范围;
的取值范围;(Ⅲ)当
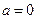 ,
,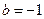 ,方程
,方程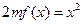 有唯一实数解,求正数
有唯一实数解,求正数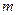 的值.
的值.略
解: (Ⅰ)依题意,知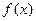 的定义域为(0,+∞),
的定义域为(0,+∞),
当 时,
时,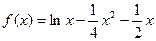 ,
,
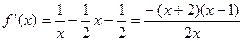 (2′)令
(2′)令 =0,
=0,
解得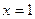 .(∵
.(∵ )
)
因为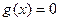 有唯一解,所以
有唯一解,所以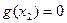 ,当
,当 时,
时,
 ,此时
,此时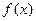 单调递增;
单调递增;
当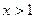 时,
时, ,此时
,此时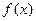 单调递减。
单调递减。
所以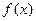 的极大值为
的极大值为 ,此即为最大值 ………4分
,此即为最大值 ………4分
(Ⅱ)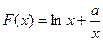 ,
,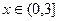 ,则有
,则有 ≤
≤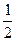 ,在
,在 上恒成立,
上恒成立,
所以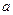 ≥
≥ ,
,
当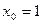 时,
时,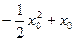 取得最大值
取得最大值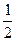 ,所以
,所以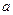 ≥
≥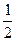 … ……8分
… ……8分
(Ⅲ)因为方程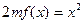 有唯一实数解,
有唯一实数解,
所以 有唯一实数解,
有唯一实数解,
设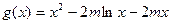 ,
,
则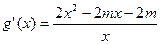 .令
.令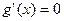 ,
, .
.
因为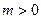 ,
, ,所以
,所以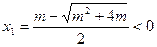 (舍去),
(舍去),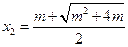 ,
,
当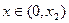 时,
时,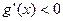 ,
,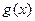 在(0,
在(0,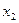 )上单调递减,
)上单调递减,
当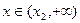 时,
时,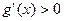 ,
,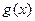 在(
在(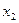 ,+∞)单调递增
,+∞)单调递增
当 时,
时, =0,
=0,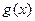 取最小值
取最小值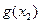 .
.
则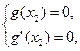 既
既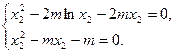
所以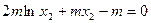 ,因为
,因为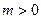 ,所以
,所以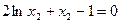 (*)
(*)
设函数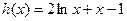 ,因为当
,因为当 时,
时,
 是增函数,所以
是增函数,所以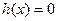 至多有一解.
至多有一解.
因为 ,所以方程(*)的解为
,所以方程(*)的解为 ,即
,即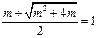 ,解得
,解得 12分
12分
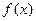 的定义域为(0,+∞),
的定义域为(0,+∞),当
 时,
时,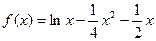 ,
,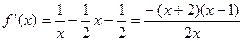 (2′)令
(2′)令 =0,
=0,解得
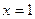 .(∵
.(∵ )
)因为
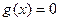 有唯一解,所以
有唯一解,所以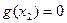 ,当
,当 时,
时, ,此时
,此时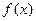 单调递增;
单调递增;当
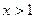 时,
时, ,此时
,此时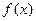 单调递减。
单调递减。所以
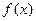 的极大值为
的极大值为 ,此即为最大值 ………4分
,此即为最大值 ………4分(Ⅱ)
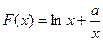 ,
,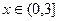 ,则有
,则有 ≤
≤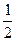 ,在
,在 上恒成立,
上恒成立,所以
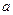 ≥
≥ ,
,
当
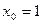 时,
时,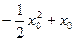 取得最大值
取得最大值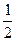 ,所以
,所以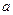 ≥
≥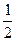 … ……8分
… ……8分(Ⅲ)因为方程
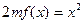 有唯一实数解,
有唯一实数解,所以
 有唯一实数解,
有唯一实数解,设
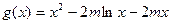 ,
,则
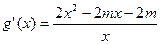 .令
.令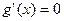 ,
, .
. 因为
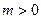 ,
, ,所以
,所以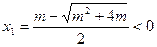 (舍去),
(舍去),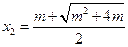 ,
,当
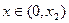 时,
时,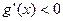 ,
,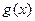 在(0,
在(0,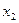 )上单调递减,
)上单调递减,当
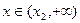 时,
时,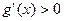 ,
,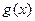 在(
在(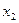 ,+∞)单调递增
,+∞)单调递增当
 时,
时, =0,
=0,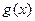 取最小值
取最小值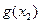 .
. 则
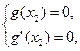 既
既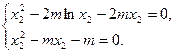
所以
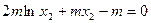 ,因为
,因为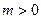 ,所以
,所以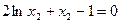 (*)
(*)设函数
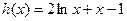 ,因为当
,因为当 时,
时, 是增函数,所以
是增函数,所以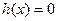 至多有一解.
至多有一解.因为
 ,所以方程(*)的解为
,所以方程(*)的解为 ,即
,即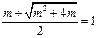 ,解得
,解得 12分
12分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
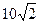 cm,面积为
cm,面积为
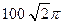 cm2的扇形铁皮制作一个无盖的圆锥形容器(衔接部分忽略不计), 该容器最多盛水多少?(结果精确到0.1 cm3)
cm2的扇形铁皮制作一个无盖的圆锥形容器(衔接部分忽略不计), 该容器最多盛水多少?(结果精确到0.1 cm3)
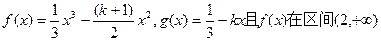 上为增函数.
上为增函数.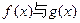 的图象有三个不同的交点,求实数k的取值范围.
的图象有三个不同的交点,求实数k的取值范围.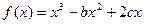 的导函数的图象关于直线
的导函数的图象关于直线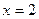 对称。
对称。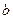 的值;
的值;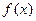 无极值,求
无极值,求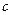 的取值范围。
的取值范围。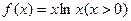 的单调递增区间是 .
的单调递增区间是 .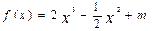 (m为常数)图像上点A处的切线与直线x一y+3=0的夹角为45o,则点A的横坐标为( )
(m为常数)图像上点A处的切线与直线x一y+3=0的夹角为45o,则点A的横坐标为( )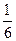
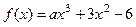 ,若
,若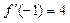 ,则实数a的值为 ( )
,则实数a的值为 ( )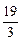
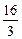
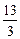

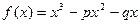 的图象与
的图象与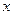 轴切于(1,0)点,则
轴切于(1,0)点,则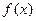 的极大值、极小值分别是
的极大值、极小值分别是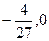
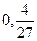
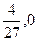
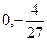
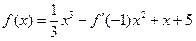 ,则
,则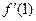 = 。
= 。