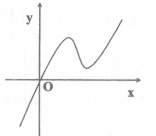
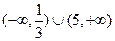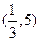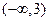题目内容
已知函数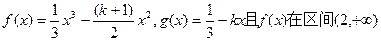 上为增函数.
上为增函数.
(1)求k的取值范围;
(2)若函数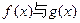 的图象有三个不同的交点,求实数k的取值范围.
的图象有三个不同的交点,求实数k的取值范围.
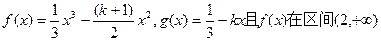 上为增函数.
上为增函数.(1)求k的取值范围;
(2)若函数
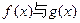 的图象有三个不同的交点,求实数k的取值范围.
的图象有三个不同的交点,求实数k的取值范围.解:(1)由题意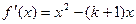 ……………………1分
……………………1分
因为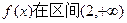 上为增函数
上为增函数
所以
 上恒成立,………………3分
上恒成立,………………3分
即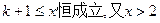
所以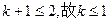 ……………………5分
……………………5分
当k=1时,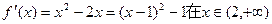 恒大于0,
恒大于0,
故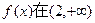 上单增,符合题意.
上单增,符合题意.
所以k的取值范围为k≤1.……………………6分
(2)设
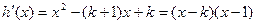
令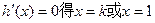 ………………8分
………………8分
由(1)知k≤1,
①当k=1时,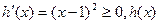 在R上递增,显然不合题意………9分
在R上递增,显然不合题意………9分
②当k<1时,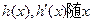 的变化情况如下表:
的变化情况如下表:
……………………11分
由于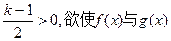 图象有三个不同的交点,
图象有三个不同的交点,
即方程
也即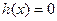 有三个不同的实根
有三个不同的实根
故需 即
即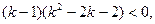 ………………13分
………………13分
所以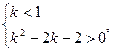 解得
解得
综上,所求k的范围为 .……………………15分
.……………………15分
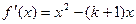 ……………………1分
……………………1分因为
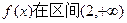 上为增函数
上为增函数所以

 上恒成立,………………3分
上恒成立,………………3分即
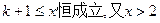
所以
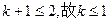 ……………………5分
……………………5分当k=1时,
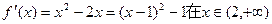 恒大于0,
恒大于0,故
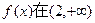 上单增,符合题意.
上单增,符合题意.所以k的取值范围为k≤1.……………………6分
(2)设

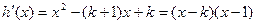
令
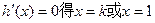 ………………8分
………………8分由(1)知k≤1,
①当k=1时,
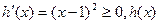 在R上递增,显然不合题意………9分
在R上递增,显然不合题意………9分②当k<1时,
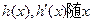 的变化情况如下表:
的变化情况如下表:| x | 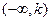 | k | (k,1) | 1 | (1,+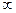 ) ) |
 | + | 0 | - | 0 | + |
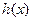 | ↗ | 极大 | ↘ | 极小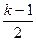 | ↗ |
由于
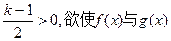 图象有三个不同的交点,
图象有三个不同的交点,即方程

也即
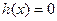 有三个不同的实根
有三个不同的实根故需
 即
即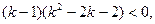 ………………13分
………………13分所以
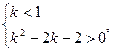 解得
解得
综上,所求k的范围为
 .……………………15分
.……………………15分略

练习册系列答案
相关题目
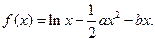
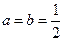 时,求
时,求 的最大值;
的最大值; ,(
,(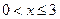 ),其图象上任意一点
),其图象上任意一点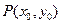 处切线的斜率
处切线的斜率 ≤
≤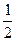 恒成立,求实数
恒成立,求实数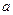 的取值范围;
的取值范围;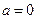 ,
,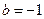 ,方程
,方程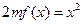 有唯一实数解,求正数
有唯一实数解,求正数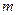 的值.
的值.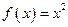 .
. 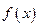 在(1,1)点处的切线
在(1,1)点处的切线 的方程;
的方程; 线
线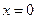 和直线
和直线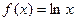 在
在 处的切线方程是
处的切线方程是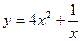 单调递增区间是( )
单调递增区间是( )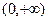

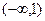
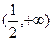
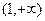
 对于
对于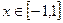 总有
总有 成立,则
成立,则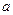 =" "
=" " 
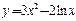 的单调减区间为 。
的单调减区间为 。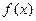 的定义域为
的定义域为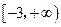 ,且
,且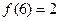 .
.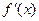 为
为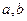 满足
满足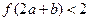 ,则
,则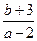 的取值范围是( )
的取值范围是( )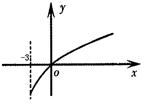
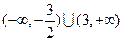
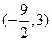
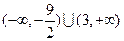

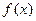 满足
满足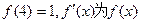 的导函数,已知
的导函数,已知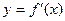 的图象如图所示,若两个正数
的图象如图所示,若两个正数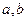 满足
满足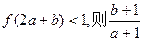 的取值范围是( )
的取值范围是( )