题目内容
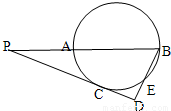
 如图,PAB是圆O的割线,AB为圆O的直径,PC为圆O的切线,C为切点,BD⊥PC于D,交圆O于点E,PA=AO=OB=1,
如图,PAB是圆O的割线,AB为圆O的直径,PC为圆O的切线,C为切点,BD⊥PC于D,交圆O于点E,PA=AO=OB=1,(1)求∠P的大小,
(2)求DE的长.
分析:(1)根据连接圆心与切点所得的半径与切线垂直,得到直角三角形,根据斜边的长度是直角边的2倍,根据直角三角形的三角函数定义,得到要求的角是30°.
(2)根据直角三角形中边长和角度,得到BD与CD的长度,根据DC是圆的一条切线,DEB是圆的一条割线,应用切割线定理,列出比例式得到结果.
(2)根据直角三角形中边长和角度,得到BD与CD的长度,根据DC是圆的一条切线,DEB是圆的一条割线,应用切割线定理,列出比例式得到结果.
解答:解:(1)连接OC,
∵PA=AO=OC=1,
∴PO=2OC,
∴∠P=30°,
(2)∵在直角三角形中,PB=3,∠P=30°,
∴BD=
,
PD=
,
∴CD=
,
∵DC是圆的一条切线,DEB是圆的一条割线,
∴DC2=DE•DB
∴DE=
=
=
答:(1)角P的度数是30°,
(2)DE的长是
∵PA=AO=OC=1,
∴PO=2OC,
∴∠P=30°,
(2)∵在直角三角形中,PB=3,∠P=30°,
∴BD=
| 3 |
| 2 |
PD=
3
| ||
| 2 |
∴CD=
| ||
| 2 |
∵DC是圆的一条切线,DEB是圆的一条割线,
∴DC2=DE•DB
∴DE=
| DC2 |
| DB |
| ||
|
| 1 |
| 2 |
答:(1)角P的度数是30°,
(2)DE的长是
| 1 |
| 2 |
点评:本题考查与圆有关的比例线段,考查特殊的直角三角形中边和角和角间的关系,本题是一个基础题,解题的关键是抓住含有30°角的直角三角形的特征.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
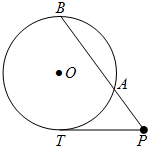 (几何证明选讲选做题)如图,PT是圆O的切线,PAB是圆O的割线,若PT=2,PA=1,∠P=60o,则圆O的半径r=
(几何证明选讲选做题)如图,PT是圆O的切线,PAB是圆O的割线,若PT=2,PA=1,∠P=60o,则圆O的半径r=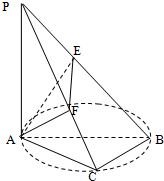 如图,AB是圆O的直径,C是圆O上的点,PA垂直于圆O所在平面,AE⊥PB于E,AF⊥PC于F
如图,AB是圆O的直径,C是圆O上的点,PA垂直于圆O所在平面,AE⊥PB于E,AF⊥PC于F (2011•通州区一模)如图.AB是圆O的弦,弦PQ平行于过点B的切线BT,AP的延长线交切线BT于点M,PA=3PM=6.∠PAB=30°.则∠QAB的度数为
(2011•通州区一模)如图.AB是圆O的弦,弦PQ平行于过点B的切线BT,AP的延长线交切线BT于点M,PA=3PM=6.∠PAB=30°.则∠QAB的度数为