题目内容
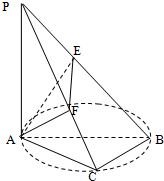 如图,AB是圆O的直径,C是圆O上的点,PA垂直于圆O所在平面,AE⊥PB于E,AF⊥PC于F
如图,AB是圆O的直径,C是圆O上的点,PA垂直于圆O所在平面,AE⊥PB于E,AF⊥PC于F求证:(1)BC⊥AF;
(2)平面AEF⊥平面PAB;
(3)AB=2,BC=
| 2 |
| 6 |
分析:(1)由已知中PA垂直于圆O所在平面,易得PA⊥BC,再由圆周角定理的推论可得AC⊥BC,结合线面垂直的判定字定理可得BC⊥平面PAC,进而由线面垂直的性质得到BC⊥AF;
(2)由已知BC⊥AF,AF⊥PC,BC,PC在平面PBC中交于C,可得AF⊥平面PBC,进而得到AF⊥PB,结合AE⊥PB及线面垂直的判定定理可得PB⊥平面AEF,再由面面垂直的判定定理即可得到平面AEF⊥平面PAB;
(3)由已知中AB=2,BC=
,PB=
,我们求出各个面的面积,进而求出各个面积的和,即可得到答案.
(2)由已知BC⊥AF,AF⊥PC,BC,PC在平面PBC中交于C,可得AF⊥平面PBC,进而得到AF⊥PB,结合AE⊥PB及线面垂直的判定定理可得PB⊥平面AEF,再由面面垂直的判定定理即可得到平面AEF⊥平面PAB;
(3)由已知中AB=2,BC=
| 2 |
| 6 |
解答:证明:(1)由题意可得:
又AC,PA在平面PAC中交于A
(2)由BC⊥AF,AF⊥PC,BC,PC在平面PBC中交于C
∴AF⊥平面PBC
又PB?平面PBC
(3)∵AB=2,BC=
,PB=
,
∴AC=
,PA=
,PC=2
∴S△ABC=1,S△PAC=1,S△PAB=
,S△PCB=
∴S=2+2
.
|
|
又AC,PA在平面PAC中交于A
|
(2)由BC⊥AF,AF⊥PC,BC,PC在平面PBC中交于C
∴AF⊥平面PBC
又PB?平面PBC
|
(3)∵AB=2,BC=
| 2 |
| 6 |
∴AC=
| 2 |
| 2 |
∴S△ABC=1,S△PAC=1,S△PAB=
| 2 |
| 2 |
∴S=2+2
| 2 |
点评:本题考查的知识点是平面与平面垂直的判定,直线与平面垂直的性质,棱锥的表面积,其中熟练掌握空间线面垂直、面面垂直、线线垂直之间关系的转化是解答本题的关键.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目


 如图,直三棱柱的一个底面ABC内接于圆O,AB是圆O的直径.
如图,直三棱柱的一个底面ABC内接于圆O,AB是圆O的直径.



 与直线
与直线 的夹角大小为
的夹角大小为
 B.(不等式选讲)要使关于x的不等式
B.(不等式选讲)要使关于x的不等式 在实数
在实数