题目内容
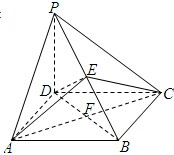 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,四边形ABCD是菱形,AC=6,BD=6
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,四边形ABCD是菱形,AC=6,BD=6| 3 |
(1)求证:AC⊥DE;
(2)当△AEC面积的最小值是9时,求证:EC⊥平面PAB.
考点:直线与平面垂直的判定,直线与平面垂直的性质
专题:证明题,空间位置关系与距离
分析:(1)连接BD,设AC与BD相交于点F.由已知中在四棱锥P-ABCD中,PD⊥平面ABCD,四边形ABCD是菱形,我们易得AC⊥BD,PD⊥AC,由线面垂直的判定定理可以得AC⊥平面PDB,再由线面垂直的性质定理,即可得到AC⊥DE;
(2)利用△AEC面积的最小值是9,求出EF,再利用线面垂直的判定定理可得结论.
(2)利用△AEC面积的最小值是9,求出EF,再利用线面垂直的判定定理可得结论.
解答:
解:(1)证明:连接BD,设AC与BD相交于点F.
因为四边形ABCD是菱形,所以AC⊥BD.
又因为PD⊥平面ABCD,AC?平面ABCD,所以PD⊥AC.
而AC∩BD=F,所以AC⊥平面PDB.
E为PB上任意一点,DE?平面PBD,所以AC⊥DE.
(2)证明:连ED.
由(1),知AC⊥平面PDB,EF?平面PBD,所以AC⊥EF.
S△ACE=
AC•AF,在△ACE面积最小时,EF最小,则EF⊥PB,
所以S△ACE=9,
×6×EF=9,解得EF=3,
由PB⊥EF且PB⊥AC得PB⊥平面AEC,则PB⊥EC,
又由EF=AF=FC=3得EC⊥AE,而PB∩AE=E,故EC⊥平面PAB.
因为四边形ABCD是菱形,所以AC⊥BD.
又因为PD⊥平面ABCD,AC?平面ABCD,所以PD⊥AC.
而AC∩BD=F,所以AC⊥平面PDB.
E为PB上任意一点,DE?平面PBD,所以AC⊥DE.
(2)证明:连ED.
由(1),知AC⊥平面PDB,EF?平面PBD,所以AC⊥EF.
S△ACE=
| 1 |
| 2 |
所以S△ACE=9,
| 1 |
| 2 |
由PB⊥EF且PB⊥AC得PB⊥平面AEC,则PB⊥EC,
又由EF=AF=FC=3得EC⊥AE,而PB∩AE=E,故EC⊥平面PAB.
点评:本题考查线面垂直的判定与性质,考查学生空间想象能力,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
小明和同学们从学校出发到一家商场去买学习用具,一路谈笑风声,不知不觉走过了商场,这时离学校5.6千米,他们马上往回走0.4千米,则学校与商场的距离是( )
| A、6千米 |
| B、5.2千米 |
| C、5.64千米 |
| D、5.56千米 |
设双曲线的一个焦点为F,虚轴的一个端点为B,如果直线FB与该双曲线的一条渐近线垂直,那么此双曲线的离心率为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|