题目内容
15.定义在[-1,1]上的函数f(x)满足:①对任意a,b∈[-1,1],且a+b≠0,都有$\frac{f(a)+f(b)}{a+b}$>0成立;②f(x)在[-1,1]上是奇函数,且f(1)=1.(1)求证:f(x)在[-1,1]上是单调递增函数;
(2)解关于x不等式f(x)<f($\frac{1}{2}$x+1);
(3)若f(x)≤m2-2am-2对所有的x∈[-1,1]及a∈[-1,1]恒成立,求实数m的取值范围.
分析 (1)利用函数单调性的定义进行证明:在区间[-1,1]任取x1、x2,且x1<x2,利用函数为奇函数的性质结合已知条件中的分式,可以证得f(x1)-f(x2)<0,所以函数f(x)是[-1,1]上的增函数.
(2)根据(1)中单调性,可得-1≤x<$\frac{1}{2}$x+1≤1,解得答案;
(3)根据函数f(x)≤m2-2am-2对所有的x∈[-1,1],a∈[-1,1]恒成立,说明f(x)的最大值1小于或等于右边,因此先将右边看作a的函数,m为参数系数,解不等式组,即可得出m的取值范围.
解答 解:(1)任取x1、x2∈[-1,1],且x1<x2,
则f(x1)-f(x2)=f(x1)+f(-x2)
∵$\frac{f({x}_{1})+f(-{x}_{2})}{{x}_{1}-{x}_{2}}$>0,x1-x2<0,
∴f(x1)-f(x2)<0.
则f(x)是[-1,1]上的增函数.
(2)若f(x)<f($\frac{1}{2}$x+1),则-1≤x<$\frac{1}{2}$x+1≤1,
解得:x∈[-1,0],
故不等式f(x)<f($\frac{1}{2}$x+1)的解集为[-1,0];
(3)要使f(x)≤m2-2am-2对所有的x∈[-1,1],a∈[-1,1]恒成立,
只须f(x)max≤m2-2am-2,即1≤m2-2am-2对任意的a∈[-1,1]恒成立,
亦即m2-2am-3≥0对任意的a∈[-1,1]恒成立.
令g(a)=m2-2am-3,
只须$\left\{\begin{array}{l}g(-1)={m}^{2}+2m-3≥0\\ g(1)={m}^{2}-2m-3≥0\end{array}\right.$,
解得m≤-3或m≥3.
点评 本题考查了抽象函数的单调性与函数的值域、不等式恒成立等知识点,属于中档题,解题时应该注意题中的主元与次元的处理.

| A. |  | B. |  | C. |  | D. |  |
| A. | 24种 | B. | 30种 | C. | 36种 | D. | 34种 |
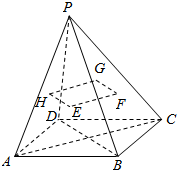 如图所示,已知四边形ABCD是平行四边形,P点是四边形ABCD所在平面外一点,连接PA、PB、PC、PD,设点E、F、G、H分别为△PAB、△PBC、△PCD、△PDA的重心.试用向量法证明E、F、G、H四点共面.
如图所示,已知四边形ABCD是平行四边形,P点是四边形ABCD所在平面外一点,连接PA、PB、PC、PD,设点E、F、G、H分别为△PAB、△PBC、△PCD、△PDA的重心.试用向量法证明E、F、G、H四点共面. ,
, ,
, .若
.若 ,则实数
,则实数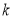 的值等于 .
的值等于 .