题目内容
6.已知角α终边经过点P($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),则cosα=$\frac{1}{2}$,sinα=$\frac{\sqrt{3}}{2}$,tanα=$\sqrt{3}$,cotα=$\frac{\sqrt{3}}{3}$,secα=2,cscα=$\frac{2\sqrt{3}}{3}$.分析 由条件利用任意角的三角函数的定义,求得要求式子的值.
解答 解:角α终边经过点P($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),则x=$\frac{1}{2}$,y=$\frac{\sqrt{3}}{2}$,r=|OP|=1,
∴cosα=x=$\frac{1}{2}$,sinα=y=$\frac{\sqrt{3}}{2}$,tanα=$\frac{y}{x}$=$\sqrt{3}$,cotα=$\frac{x}{y}$=$\frac{\sqrt{3}}{3}$,
secα=$\frac{1}{cosα}$=2,cscα=$\frac{1}{sinα}$=$\frac{2\sqrt{3}}{3}$,
故答案为:$\frac{1}{2}$;$\frac{\sqrt{3}}{2}$;$\sqrt{3}$;$\frac{\sqrt{3}}{3}$;2;$\frac{2\sqrt{3}}{3}$.
点评 本题主要考查任意角的三角函数的定义,属于基础题.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
14.已知正项等比数列{an},且a2a10=2a52,a3=1,则a4=( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{2}$ | D. | 2 |
11.已知a>0,不等式组$\left\{\begin{array}{l}{x≥0}\\{y≤0}\\{y≥a(x-2)}\end{array}\right.$,表示的平面区域的面积为1,则a的值为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
18.不等式($\frac{1}{3}$)x-1≤0的解集是( )
| A. | (-∞,1] | B. | (-∞,0] | C. | [1,+∞) | D. | [0,+∞) |
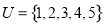 , 集合
, 集合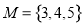 ,
, 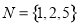 , 则集合
, 则集合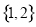 可以表示为
可以表示为 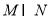 B.
B.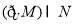
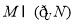 D.
D.