题目内容
6.若logac+logbc=0(c≠1),则ab+c-abc=1.分析 根据题意,结合对数的运算性质,由logac+logbc=0(c≠1)可得lga=-lgb,分析可得ab=1,代入ab+c-abc中计算可得答案.
解答 解:根据题意,若logac+logbc=0(c≠1),
必有$\frac{lgc}{lga}$+$\frac{lgc}{lgb}$=0,即lga=-lgb,
变形可得a=$\frac{1}{b}$,即ab=1,
ab+c-abc=1+c-c=1;
故答案为:1.
点评 本题考查对数的运算,涉及换底公式的运用,解题的关键是由logac+logbc=0得到a、b的关系.

练习册系列答案
相关题目
14.已知正项等比数列{an},且a2a10=2a52,a3=1,则a4=( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{2}$ | D. | 2 |
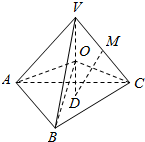 如图所示,正四面体V-ABC的高VD的中点为O,VC的中点为M.
如图所示,正四面体V-ABC的高VD的中点为O,VC的中点为M.