题目内容
【题目】已知在锐角△ABC中,a,b,c为角A,B,C所对的边,且(b﹣2c)cosA=a﹣2acos2 ![]() .
.
(1)求角A的值;
(2)若a= ![]() ,则求b+c的取值范围.
,则求b+c的取值范围.
【答案】
(1)解:在锐角△ABC中,根据(b﹣2c)cosA=a﹣2acos2 ![]() =a﹣2a
=a﹣2a ![]() ,
,
利用正弦定理可得 (sinB﹣2sinC)cosA=sinA(﹣cosB),
即 sinBcosA+cosBsinA=2sinCcosA,即sin(B+A)=2sinCcosA,
即sinC=2sinCcosA,∴cosA= ![]() ,∴A=
,∴A= ![]()
(2)解:若a= ![]() ,则由正弦定理可得
,则由正弦定理可得 ![]() =
= ![]() =2,
=2,
∴b+c=2(sinB+sinC)=2[sinB+sin( ![]() ﹣B)]=3sinB+
﹣B)]=3sinB+ ![]() cosB=2
cosB=2 ![]() sin(B+
sin(B+ ![]() ).
).
由于 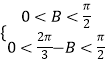 ,求得
,求得 ![]() <B<
<B< ![]() ,∴
,∴ ![]() <B+
<B+ ![]() <
< ![]() .
.
∴sin(B+ ![]() )∈(
)∈( ![]() ,1],∴b+c∈(3,2
,1],∴b+c∈(3,2 ![]() ]
]
【解析】(1)在锐角△ABC中,根据条件利用正弦定理可得 (sinB﹣2sinC)cosA=sinA(﹣cosB),化简可得cosA = ![]() ,由此可得A的值.(2)由正弦定理可得
,由此可得A的值.(2)由正弦定理可得 ![]() =
= ![]() =2,可得 b+c=2(sinB+sinC)=2
=2,可得 b+c=2(sinB+sinC)=2 ![]() sin(B+
sin(B+ ![]() ).
).
再由  ,求得B的范围,再利用正弦函数的定义域和值域求得b+c的取值范围.
,求得B的范围,再利用正弦函数的定义域和值域求得b+c的取值范围.
【考点精析】本题主要考查了正弦定理的定义的相关知识点,需要掌握正弦定理:![]() 才能正确解答此题.
才能正确解答此题.

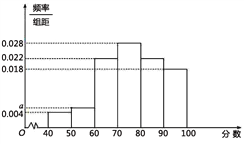
【题目】毕节市正实施“五城同创”计划。为搞好卫生维护工作,政府招聘了200名市民志愿者,按年龄情况进行统计的频率分布表和频率分布直方图如下:
分组(岁) | 频数 | 频率 |
[30,35) | 20 | 0.1 |
[35,40) | 20 | 0.1 |
[40,45) | ① | 0.2 |
[45,50) | ② | ③ |
[50,55] | 40 | 0.2 |
合计 | 200 | 1 |
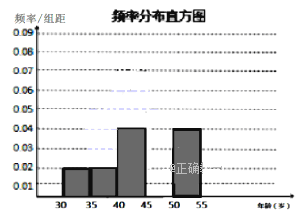
(1)频率分布表中的①②③位置应填什么数?补全频率分布直方图;
(2)根据频率分布直方图估计这200名志愿者的平均年龄.