题目内容
【题目】已知某中学高三文科班学生共有800人参加了数学与地理的水平测试，学校决定利用随机数表法从中抽取100人进行成绩抽样调查，先将800人按001，002，…，800进行编号
（1）如果从第8行第7列的数开始向右读，请你依次写出最先检查的3个人的编号；（下面摘取了第7行到第9行）
84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76
63 01 63 78 59 16 95 56 67 19 98 10 50 71 75 12 86 73 58 07 44 39 52 38 79
33 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 54
（2）抽取的100人的数学与地理的水平测试成绩如下表：
成绩分为优秀、良好、及格三个等级；横向，纵向分别表示地理成绩与数学成绩，例如：表中数学成绩为良好的共有
.
①若在该样本中，数学成绩优秀率是30%，求
的值：
人数 | 数学 | |||
优秀 | 良好 | 及格 | ||
地理 | 优秀 | 7 | 20 | 5 |
良好 | 9 | 18 | 6 | |
及格 |
| 4 |
| |
②在地理成绩及格的学生中，已知
， 
，求数学成绩优秀的人数比及格的人数少的概率.
【答案】（1）785，667，199; （2）
【解析】试题分析：（1）从第8行第7列的数开始向右读，最先检查的编号为：785，916，955，667，199，…去除大于800的编号，可得最先检查的3个人的编号；（2）①根据数学成绩优秀率是
，构造关于
的方程，解方程可得
值，进而根据抽取样本容量为100，可得
值；②求出满足
， 
的基本事件总数及满足数学成绩优秀的人数比及格的人数少的基本事件个数，代入古典概型概率计算公式，可得答案.
试题解析：（1）785，667，199.
（2）①
，∴
； 
.
②
.
因为
， 
，所以
的搭配：
， 
， 
， 
， 
， 
， 
， 
， 
， 
， 
， 
， 
， 
，共有14种.
设
， 
时，数学成绩优秀的人数比及格的人数少为事件
， 
.
事件
包括： 
， 
，共2个基本事件；
，数学成绩优秀的人数比及格的人数少的概率为
.
【题目】“累计净化量(CCM)”是空气净化器质量的一个重要衡量指标，它是指空气净化器从开始使用到净化效率为
时对颗粒物的累计净化量(单位：克)．根据国家标准，对空气净化器的累计净化量(CCM)有如下等级划分：
累计净化量（克） |
|
|
| 12以上 |
等级 |
|
|
|
|
已知某批空气净化器共
台，其累计净化量都分布在区间
内，为了解其质量，随机抽取了
台净化器作为样本进行估计，按照
，
，
，
，
均匀分组，其中累计净化量在的所有数据有：
，
，
，
，
和
，并绘制了如下频率分布直方图．
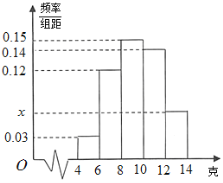
（1）求
的值及频率分布直方图中
的值；
（2）以样本估计总体，试估计这批空气净化器（共2000台）中等级为
的空气净化器有多少台？
（3）从累计净化量在的样本中随机抽取2台，求恰好有1台等级为的概率．
