题目内容
抛物线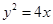
的焦点到双曲线
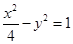的渐近线的距离是 ．
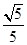
解析试题分析：抛物线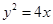的焦点为
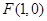，双曲线的渐近线为
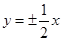，即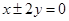
，所求距离为
．
考点：点到直线的距离公式．
练习册系列答案
名校课堂系列答案
相关题目
名校课堂系列答案题目内容
抛物线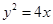的焦点到双曲线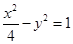的渐近线的距离是 ．
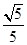
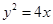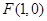解析试题分析：抛物线的焦点为，双曲线的渐近线为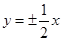，即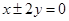，所求距离为．
考点：点到直线的距离公式．
名校课堂系列答案
，则此双曲线的离心率为 
的焦点与双曲线
的左焦点重合，则双曲线的两条渐近线的夹角为 .
的离心率为
，则实数m的值为 ．
和直线
，过点
且与直线
相切的动圆圆心为点
，记点
.
的坐标为
，直线
（
，且
）与抛物线
，相交于
、
两点，直线
、
分别交直线
于点
、
试判断以线段
为直径的圆是否恒过两个定点？若是，求这两个定点的坐标；若不是，说明理由.
的焦点坐标是 .
＝1的中心为顶点，且以该双曲线的右焦点为焦点的拋物线方程是__________．
＝1(a，b＞0)的左、右焦点，B是虚轴的端点，直线F1B与C的两条渐近线分别交于P、Q两点，线段PQ的垂直平分线与x轴交于点M.若MF2＝F1F2，则C的离心率是________．