题目内容
若中心在原点、焦点在坐标轴上的双曲线的一条渐近线方程为 ,则此双曲线的离心率为
,则此双曲线的离心率为
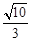 或
或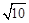
解析试题分析:由题意的: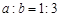 或
或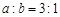 ,所以
,所以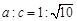 或
或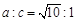 ,因此双曲线的离心率为
,因此双曲线的离心率为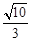 或
或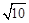
考点:双曲线的渐近线

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
题目内容
若中心在原点、焦点在坐标轴上的双曲线的一条渐近线方程为 ,则此双曲线的离心率为
,则此双曲线的离心率为
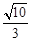 或
或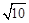
解析试题分析:由题意的: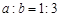 或
或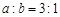 ,所以
,所以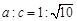 或
或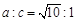 ,因此双曲线的离心率为
,因此双曲线的离心率为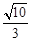 或
或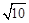
考点:双曲线的渐近线

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案