Question

6．一空间几何体的三视图如图所示，则该几何体所有棱长的取值集合为$\left\{{2，3，\sqrt{5}}\right\}$；
 

Answer 1

分析 观察几何体的三视图，还原为几何体，然后根据空间线段关系求棱长．

解答 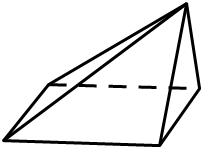解：由题意，此三视图对应的几何体如图
过E作EF⊥BC，由已知可得EF⊥平面ABCD，并且AB=EF=2，BF=FC=1，所以CE=BE=$\sqrt{E{F}^{2}+B{F}^{2}}=\sqrt{5}$，连接AF，则DE=AE=$\sqrt{E{F}^{2}+A{F}^{2}}=\sqrt{4+5}=3$，

所以该几何体所有棱长的取值集合为$\left\{{2，3，\sqrt{5}}\right\}$；
故答案为：$\left\{{2，3，\sqrt{5}}\right\}$．

点评 本题考查了由几何体的三视图还原为几何体，考查了学生的空间想象能力以及空间线段长度的求法．